眼瞅着这学期也快接近尾声了,也在讲我越来越不熟悉的东西了...
核平滑与局部方法
1. 核平滑器
(1) K-NN(K近邻)
KNN的思想已经说过很多遍了,大致就是找点x的k个近邻,然后取其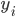 平均值作为x点y的预测值
平均值作为x点y的预测值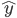 。不过这里我们就在想了,可不可以加权呀~于是从最简单的
。不过这里我们就在想了,可不可以加权呀~于是从最简单的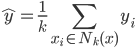 ,我们给他按距离算个加权平均:
,我们给他按距离算个加权平均: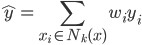 ,其中
,其中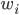 代表权重,离x点越近越大,越远越小。这样听起来更make sense一点嘛~近朱者赤,近墨者黑。
代表权重,离x点越近越大,越远越小。这样听起来更make sense一点嘛~近朱者赤,近墨者黑。
(2) 单峰函数
顾名思义,就是长得像一个山峰的函数,比如我们最经典的正态钟型函数,或者翻过来的二次抛物线函数等等。
(3) 权重(按距离)
我们定义权重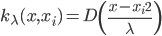 ,再进一步归一化:
,再进一步归一化: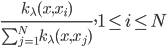 。
。
多维的情况下,写成矩阵形式就是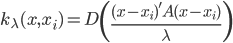 ,其中A为正定对角阵,然后我们就可以加权了。
,其中A为正定对角阵,然后我们就可以加权了。
2. 局部方法
(1) 一般概念
我们有数据集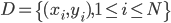 ,然后定义函数族
,然后定义函数族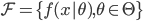 。再定义损失函数
。再定义损失函数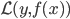 , 我们的目标就是最小化
, 我们的目标就是最小化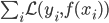 。
。
相应的引入了加权的概念之后,我们就可以定义加权损失函数: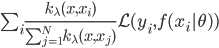 ,然后对于每个x做优化,寻找使其最小化的
,然后对于每个x做优化,寻找使其最小化的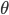 。
。
(2) 具体例子
(i) 局部回归: 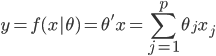 ,则损失函数为
,则损失函数为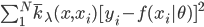 ,其中
,其中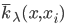 代表已经归一化的权重。
代表已经归一化的权重。
在线性的情况下,我们有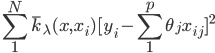 ,有点类似于我们常见的加权最小二乘法。这里的思想也是,在x点附近的点权重会比较大,离x远的权重则比较小,整体感觉就是在x点附近做了一个回归分析。
,有点类似于我们常见的加权最小二乘法。这里的思想也是,在x点附近的点权重会比较大,离x远的权重则比较小,整体感觉就是在x点附近做了一个回归分析。
(ii) 局部似然:和局部回归蛮像的,只是把损失函数换成(对数)似然函数,即从最大化 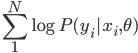 到现在的最大化加权似然函数
到现在的最大化加权似然函数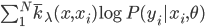 。
。
3. 密度估计与分类
(1) 密度与分类: 我们有x和观测结果G的联合分布: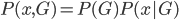 ,其中
,其中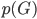 为先验的结果分布,在有K类结果的情况下,写成
为先验的结果分布,在有K类结果的情况下,写成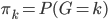 。这样,也可以写开为
。这样,也可以写开为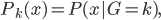 其中
其中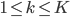 。
。
反过来,后验概率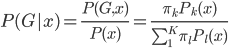 ,所以我们有贝叶斯分类器
,所以我们有贝叶斯分类器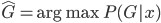 。
。
(2) 密度估计
为了使用贝叶斯分类器,我们需要先对密度进行估计。
(i) 直方图: 最简单的就是根据直方图来估计密度,这个没什么好说的...
(ii) 核估计方法(Parzen):Parzen提出的核密度估计为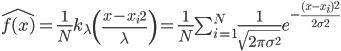 ,该估计当
,该估计当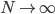 且
且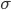 在减小的时候,收敛于
在减小的时候,收敛于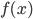 。
。
4. 核作为基函数
密度函数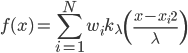 ,然后定义函数族
,然后定义函数族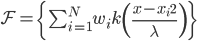 ,则其中
,则其中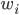 我iyigexianxingde参数,
我iyigexianxingde参数,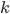 为指定的函数类,
为指定的函数类,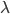 亦为函数参数。这样的话我们有三个函数的参数,指定某一个便可以简化函数形式。不过这里的问题是,没有很好的算法来求解优化问题。比如对于正态分布,我们以写出来
亦为函数参数。这样的话我们有三个函数的参数,指定某一个便可以简化函数形式。不过这里的问题是,没有很好的算法来求解优化问题。比如对于正态分布,我们以写出来 ,然后的求解就比较复杂了。
,然后的求解就比较复杂了。
上面的两个是非参数方法,下面说一些参数方法。
(iii) 混合模型(GMM, Gauss Mixed Model)
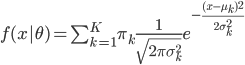 ,其中参数有
,其中参数有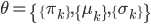 ,然后可以利用最大似然准则,最大化
,然后可以利用最大似然准则,最大化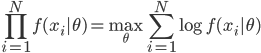 ,具体算法可用EM,下节课详述。
,具体算法可用EM,下节课详述。
-----稍稍跑题------
GMM,我印象中它怎么是 Generalized Moment Method, 广义矩估计呢?果然是被计量经济学祸害太深了...
2 replies on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(九)”
“则其中wiwi我iyigexianxingde参数”
这个内容有没有一些排序问题啊,,怎么核作为基函数后面还有一个标题三,那个是密度估计与分类的方法吗