平滑splines
有数据集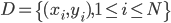 ,然后定义目标函数
,然后定义目标函数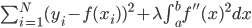 ,记为(1)
,记为(1)
式。然后我们有如下结论:使(1)最小化的解一定是分段三次多项式。
证明如下。
记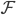 为函数族
为函数族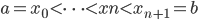 上的分段三次多项式(splines),且在首尾两段
上的分段三次多项式(splines),且在首尾两段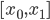 和
和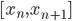 上是一次多项式,那么他一定有
上是一次多项式,那么他一定有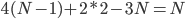 的自由度。
的自由度。
若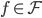 ,则当
,则当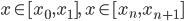 时,有
时,有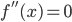 。
。
(2) 我们设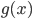 也是(1)式的解,则下面证明一定能找到
也是(1)式的解,则下面证明一定能找到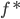 使得目标函数比
使得目标函数比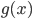 小,则
小,则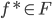 ,
,
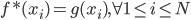 .
.
(3)记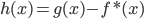 ,则
,则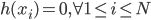
(4) 下面我们证明,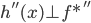 (两者内积为0),即
(两者内积为0),即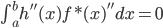 。
。
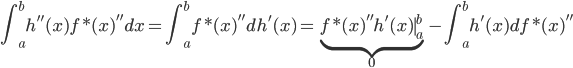
且
所以得到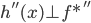 。
。
(5)有了上述结论后,我们有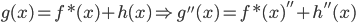 ,然后有
,然后有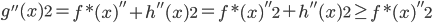 ,所以对于所有的g,我们都有其二阶导数的范数小于f的二阶导数的范数,故在(1)式中代入g总比代入f大(或者相等)。这样我们就把一个无限维的最优化问题变为了有限维。
,所以对于所有的g,我们都有其二阶导数的范数小于f的二阶导数的范数,故在(1)式中代入g总比代入f大(或者相等)。这样我们就把一个无限维的最优化问题变为了有限维。
子波分析
1. 函数的平移与缩放
平移: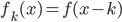
缩放: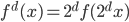
组合起来就是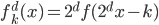 。由此,对于每个
。由此,对于每个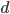 ,我们可以定义一个函数族
,我们可以定义一个函数族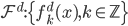 ,写成矩阵形式就是
,写成矩阵形式就是

2. Hoar函数
(1)定义: 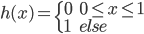 。
。
(2)Hoar函数的平滑与缩放。定义Hoar函数族为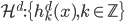 ,
,
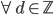 。这样我们每个
。这样我们每个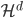 为一组(胖瘦一样)。
为一组(胖瘦一样)。
定理1(正交):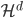 是
是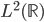 平方可积函数的一个正交基,即对于任意的
平方可积函数的一个正交基,即对于任意的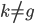 ,有
,有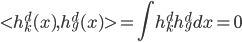 。
。
定理2(增长):随着d的增加,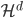 张成的闭子空间逐渐增大,且
张成的闭子空间逐渐增大,且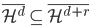 。这样,d比较小的函数一定能用d比较大的函数(正交基)来表示,比如
。这样,d比较小的函数一定能用d比较大的函数(正交基)来表示,比如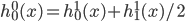 。直观的理解就是,d越大,分辨率越高。
。直观的理解就是,d越大,分辨率越高。
定理3(完备):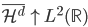
(3)定义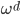 ,使
,使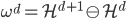 ,或者
,或者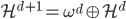 。
。
(4)定义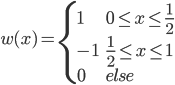 ,然后
,然后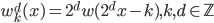 。
。
定理4:函数族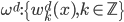 ,
,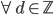 ,则
,则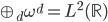 亦为完备基,且
亦为完备基,且 ,如果
,如果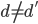 。也就是说,
。也就是说, 和
和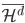 之间的空间随着d的增加,彼此正交,且所有的叠起来之后亦为完备空间。
之间的空间随着d的增加,彼此正交,且所有的叠起来之后亦为完备空间。
如此,我们称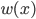 为子波(mother)而
为子波(mother)而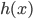 为father函数。注意,这里Hoar函数非连续。
为father函数。注意,这里Hoar函数非连续。
在更一般的场合,我们寻找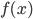 为father函数,然后定义
为father函数,然后定义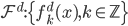 ,满足
,满足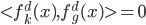 (正交),且
(正交),且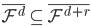 (增长),
(增长),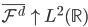 (完备)。
(完备)。
再寻找mother函数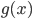 满足
满足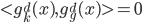 (同层次内正交)、
(同层次内正交)、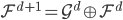 (相邻层次正交补)和
(相邻层次正交补)和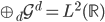 完备。
完备。
这样的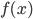 和
和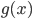 到底存不存在呢?实证结论是存在,而且很多,不过坏消息是他们的形式都不算简单。
到底存不存在呢?实证结论是存在,而且很多,不过坏消息是他们的形式都不算简单。
spline和子波分析
spline和子波分析都提供了一组线性基底,其线性组合可以定义函数类。由此,我们可以定义广义线性模型的函数族,为统计学习模型的函数族做约束。
One reply on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(八)”
好单调 大众表示不够欢乐