上海的冬天越来越冷了,这门课也越来越临近这学期结束了。这节课公式推导不多,有也是那种烂熟于胸无数次的,所以可以稍稍歪楼,不时掺杂一点八卦什么的。
BootStrap
1. 定义
BootStrap的基本思想就仨字:重抽样。先开始八卦~
跟高斯窥探天机猜出来正态分布的密度函数表达式相似,Efron搞出来BootStrap的时候,大概也在偷偷的抿嘴而笑吧。“上帝到底掷不掷骰子呢?”,每次我们都在揣测天意,也是现在越来越有点理解为什么牛顿老先生晚年致力于神学了。每当我们猜中一次,就会有一个新的突破到来。BootStrap思想简单到如斯,以至于我的一位朋友在当高中老师的时候(可惜是美国不是中国),就尝试着跟 teenagers 介绍BootStrap思想了(貌似用的还是Econometrica上的一篇文章,我瞬间声讨“你们这群高中老师真凶残-_-||)——结果显然是我多虑了,那群熊孩子居然表示理解毫无压力!可见BootStrap这个东西是有多么的平易近人。什么测度论什么高等代数都不需要,会摸球就可以了!
顺便抄一下杨灿童鞋《那些年,我们一起追的EB》上的一段八卦:
五十多年前,Efron为 Stanford 的一本幽默杂志 Chapparal 做主编。那年,他们恶搞 (parody) 了著名杂志Playboy。估计是恶搞得太给力了,还受到当时三藩的大主教的批评。幽默的力量使 Efron 在“错误”的道路上越走越远,差点就不回Stanford 读 PhD 了。借用前段时间冰岛外长的语录:“Efron 从事娱乐时尚界的工作,是科学界的一大损失!”在关键时刻,Efron在周围朋友的关心和支持下,终于回到 Stanford,开始把他的犀利与机智用在 statistics 上。告别了娱乐时尚界的 EB,从此研究成果犹如滔滔江水,连绵不绝,citation又如黄河泛滥,一发不可收拾...
所以说嘛,天才之人做什么都是能闪光的,Efron从事科学界的工作,怕也是美国几亿人民周末娱乐的损失吧。好了,满足了你们这群越来越挑剔的读者八卦的胃口了,开始正儿八经的说BootStrap。
我们有观测数据集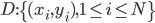 ,然后对这N个样本,进行有放回的重抽样。每轮我们还是抽N个,然后一共抽B轮(比如几百轮,话说前几天weibo上有人问“如果给你一万个人,你要做什么”,放在这里我就要他们不停的抽小球抽小球抽小球,哈哈!)。这样就得到了新的观测样本
,然后对这N个样本,进行有放回的重抽样。每轮我们还是抽N个,然后一共抽B轮(比如几百轮,话说前几天weibo上有人问“如果给你一万个人,你要做什么”,放在这里我就要他们不停的抽小球抽小球抽小球,哈哈!)。这样就得到了新的观测样本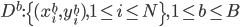 。
。
2. 应用
BootStrap几乎可以用来干各种合法的不合法的事儿,只要是跟数据估计有关的...这就如同你问一个画家,“什么最好画?”“上帝和魔鬼,因为大家都没有见过。”大家都没有那么明确的知道BootStrap的界限在哪里,所以BootStrap就被应用在各种跟估计有关的地方了。
在统计学习中,我们最常用的可能就是估计精度:对于每一个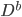 ,我们都可以得到一个预测函数
,我们都可以得到一个预测函数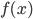 ,然后就对于给定的
,然后就对于给定的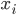 ,有B个预测值
,有B个预测值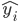 ,这样就可以做直方图什么的,还可以排排序算出来
,这样就可以做直方图什么的,还可以排排序算出来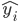 的置信区间。
的置信区间。
最大似然估计(MLE)
我们有一族密度函数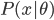 ,其中
,其中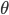 为参数集,可不止一个参数。按照概率的定义,我们有
为参数集,可不止一个参数。按照概率的定义,我们有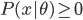 ,而且
,而且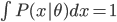 。
。
数据方面,我们有一组数据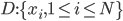 ,为\emph{i.i.d}(独立同分布)。
,为\emph{i.i.d}(独立同分布)。
这样就可以写出来似然函数: 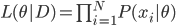 ,从而可以写出来对数似然函数:
,从而可以写出来对数似然函数: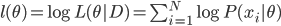 。接下来驾轻就熟的,我们就有最大似然估计量:
。接下来驾轻就熟的,我们就有最大似然估计量: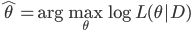 。
。
最大似然估计之所以这么受欢迎,主要是他有一个非常好的性质:一致性,即当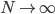 ,估计值
,估计值 收敛于真值
收敛于真值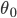 。
。
仅仅渐进一致还不够,我们当然更喜欢的是MLE的附加优良性质:渐进正态,即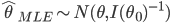 ,其中
,其中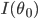 称为信息矩阵,定义为
称为信息矩阵,定义为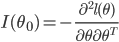 。实际中,如果我们不知道真值
。实际中,如果我们不知道真值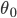 ,则会用估计值来代替正态分布中的参数。(没想到事隔这么多年,我居然又手动推导了一遍MLE...真的是,我跟统计的缘分怎么这么纠缠不断呀)。
,则会用估计值来代替正态分布中的参数。(没想到事隔这么多年,我居然又手动推导了一遍MLE...真的是,我跟统计的缘分怎么这么纠缠不断呀)。
MLE大都要求数值解的,少数情况下可以求解解析解。比如正态分布。
正态分布的密度函数为: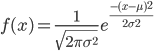 ,所以我们有对数似然函数:
,所以我们有对数似然函数:
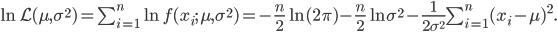
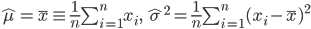
还有一个特例是正态线性回归模型(Gauss-Markov),即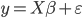 ,其中
,其中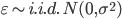 ,这个就和OLS的BLUE性质蛮像了,MLE和OLS对于此种情形估计值是完全一样的。所以说高斯王子在搞出OLS的时候,也是各种深思熟虑过的...揣测上帝的“旨意”也不是件信手拈来的事儿的。
,这个就和OLS的BLUE性质蛮像了,MLE和OLS对于此种情形估计值是完全一样的。所以说高斯王子在搞出OLS的时候,也是各种深思熟虑过的...揣测上帝的“旨意”也不是件信手拈来的事儿的。
简单情形下,我们可以直接求得估计量的置信区间,但是在复杂的情形下,就只能用BootStrap了。人们的思路就从传统的数学推倒,越来越多的转换到计算能力了。有的时候稍稍感觉这更符合统计学的思维——归纳嘛,这也是统计学在computer
area和数学渐行渐远的表现之一么?
吴老师总结了一句话:BootStrap类方法,就是思想简单、实际有效,虽然不知道为什么...
模型平均
模型平均也是有点延续上面的BootStrap思想,就是我有很多重抽样出来的模型之后,要怎么平均这些结果来找出最优模型的。
1. Bagging方法。 这个就有点直截了当了。利用BootStrap,我可以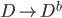 ,然后自然收集了一堆
,然后自然收集了一堆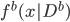 ,所以简单一点就平均一下:
,所以简单一点就平均一下: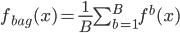
2. Stacking方法。这个就稍稍动了一点心思,直接平均看起来好简单粗暴呀,还是加权平均一下比较细致一点。所以: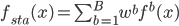 ,其中权重
,其中权重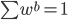 。实际操作中,
。实际操作中,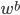 的选取也是一个蛮tricky的事儿。可以利用validation集来优化...
的选取也是一个蛮tricky的事儿。可以利用validation集来优化...
3. Bumpping (优选)方法。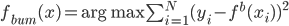 ,即在所有的
,即在所有的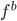 中,选择最好的那个,使得一定标准下的损失最小。
中,选择最好的那个,使得一定标准下的损失最小。
话说,Machine learning或者统计学习,无非就是四件事儿:数据(D)、函数族(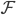 )、准则(
)、准则(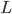 )、算法(A)。说来说去,每一样改进都是在这四个的某一方面或者某几方面进行提升的。
)、算法(A)。说来说去,每一样改进都是在这四个的某一方面或者某几方面进行提升的。
2 replies on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十一)”
“Machine learning或者统计学习,无非就是四件事儿:数据(D)、函数族( F )、准则( L )、算法(A)。说来说去,每一样改进都是在这四个的某一方面或者某几方面进行提升的。”
太精辟了!特地登陆赞一下!同时感谢楼主分享笔记!
哈哈,回头看看笔记也有种温故而知新的感觉....