本学期最后一堂课的笔记...就这样,每周上班的时候都没有惦念的了,我是有多么喜欢教室和课堂呀。或者说,真的是太习惯学校的生活方式了吧...
这一节主要是在上一节的基础上,介绍一些可加模型或者树模型的相关(改进)方法。
MARS
MARS全称为Multivarible Adaptive Regression Splines,看名字就能猜出来大致他是做啥的。MARS这家伙与CART一脉相承(话说CART的竞争对手就是大名鼎鼎的C4.5)。不过,还是先说一下MARS到底是怎么玩的吧。
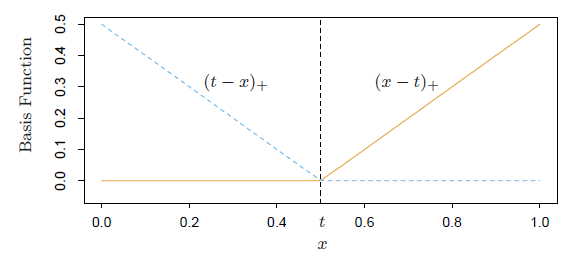
数据集依旧记作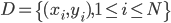 ,然后就是splines的思想:我们定义
,然后就是splines的思想:我们定义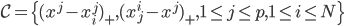 ,其中
,其中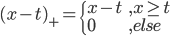 和
和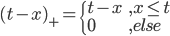 ,画出图形来就是:
,画出图形来就是:
这样就可以定义I函数了: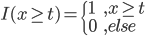 ,以及
,以及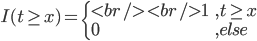 ,越来越有spines味道了是不是?
,越来越有spines味道了是不是?
之后就是定义f函数: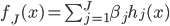 ,然后有意思的就来了:
,然后有意思的就来了: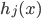 是
是 中函数或者几个函数的乘积,选定了
中函数或者几个函数的乘积,选定了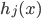 之后我们就可以用最小二乘法来求解相应的
之后我们就可以用最小二乘法来求解相应的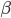 了。然后在接下来的每一步,我们都添加
了。然后在接下来的每一步,我们都添加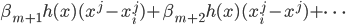 这样,一步步的,
这样,一步步的,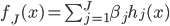 就开始增长。当我们用完了
就开始增长。当我们用完了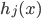 之后,显然有
之后,显然有
over-fit的嫌疑,所以开始逐步的减少一些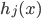 ——考虑移除那些对减少残差平方和贡献比较小的项目。沿着cross-validation的思路,就可以定义函数
——考虑移除那些对减少残差平方和贡献比较小的项目。沿着cross-validation的思路,就可以定义函数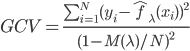 。
。
PRIM
PRIM的全称为Patient Rule Induction Method,呃看名字貌似是一种比较耐心的一步步递归的方法。果不其然,最开始就是我们要先定义“削皮”:选取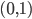 区间内任意的
区间内任意的 ,比如0.1,然后开始削皮~削皮的策略大概就是,选定一个维度,去掉这个维度比如最大10\%或者最小10\%的样本,然后看剩余部分的y均值有没有增长。总共有p个维度,所以我们有
,比如0.1,然后开始削皮~削皮的策略大概就是,选定一个维度,去掉这个维度比如最大10\%或者最小10\%的样本,然后看剩余部分的y均值有没有增长。总共有p个维度,所以我们有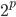 中削皮法。选择其中上升最高的方法,削皮。然后继续来一遍,直到不能再增长的时候,停止,最终得到一块“精华”(贪心的算法)。之后,我们又要开始粘贴,即再贴上去一块儿,看看是否能涨。这样我们得到一个
中削皮法。选择其中上升最高的方法,削皮。然后继续来一遍,直到不能再增长的时候,停止,最终得到一块“精华”(贪心的算法)。之后,我们又要开始粘贴,即再贴上去一块儿,看看是否能涨。这样我们得到一个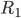 区,区域均值为
区,区域均值为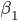 。
。
从总体中扔掉这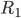 区中的样本,然后继续做下去,比如一共J次,得到J个区域(这些区域的空间可能是有交集的),这样的策略称为Bump-Hunting(肿块寻找),最终得到若干个区域,各区域中的样本均值作为
区中的样本,然后继续做下去,比如一共J次,得到J个区域(这些区域的空间可能是有交集的),这样的策略称为Bump-Hunting(肿块寻找),最终得到若干个区域,各区域中的样本均值作为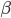 (以第一次出现的空间为准)。
(以第一次出现的空间为准)。
HME
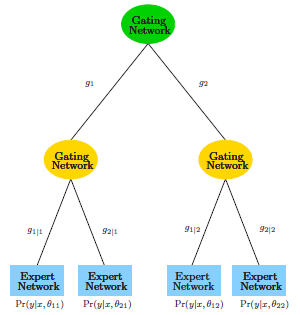
HME的全称为Hierarchical Mixture of Experts,听起来像是一个智囊团的感觉。画出来呢,就是一个树的形状。
大致的思想就是,以概率分配到各个枝条(软分类器),这样有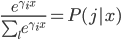 。对于最下面一层的expert
。对于最下面一层的expert
net,可以用分类树或者其他任何的分类器。对于HME,可用EM算法来解。两类的情形,就有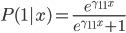 ,有点像logit的变形有没有?
,有点像logit的变形有没有?
一句话的总结呢,就是这些方法看上去合理,比较容易follow the intuition,但是树类的结构弄得很难用现有的方法证明原理和一些相关性质(完全非线性呀)。
模型的总结:广义线性模型和基函数模型
从第一章到第九章,我们探索了很多个模型。说到底,模型就是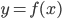 ,然后我们有参数模型
,然后我们有参数模型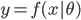 ,其中
,其中 ,
, 。
。
最简单的来说,就是线性模型,形式为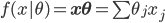 ,其中
,其中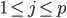 。显然,线性模型便是参数模型。
。显然,线性模型便是参数模型。
然后就是广义线性模型(GLM),我们可以先扩张x,就有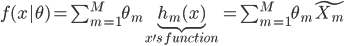 。说到底,就是已知的
。说到底,就是已知的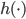 把数据从
把数据从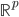 空间映射到一个新的
空间映射到一个新的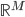 空间。然后还可以把y再广义化,用一个可逆的已知函数
空间。然后还可以把y再广义化,用一个可逆的已知函数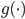 变成
变成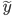 。这样,就有
。这样,就有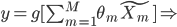
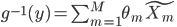 ,最终说来
,最终说来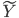 和
和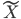 这两个空间实现了一种线性的映射关系。
这两个空间实现了一种线性的映射关系。
接下来我们就会看到一种形状很类似的树模型,但不是GLM: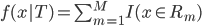 。显然这里
。显然这里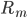 远非线性的,而且是变量。
远非线性的,而且是变量。
接着参数化,我们就有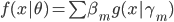 ,若
,若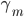 未知,即
未知,即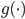 可变,则非GLM。这类的模型更适合的名字是:自适应基函数模型,即我们试图构造一些可以自适应的基函数,然后通过其线性组合构造最终的模型。这类模型经典如:树模型、GMM(高斯混合模型)、神经网络等。
可变,则非GLM。这类的模型更适合的名字是:自适应基函数模型,即我们试图构造一些可以自适应的基函数,然后通过其线性组合构造最终的模型。这类模型经典如:树模型、GMM(高斯混合模型)、神经网络等。
3 replies on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十三)”
我一路跟你看连载~~~
Thx
太赞~ 一路结合着你的笔记看esl.