梯度树提升算法(GTBA, gradient tree boosting algorithm)
继续boosting类算法哎。小小预告一下,下节课会直接跳到随机森林,老师貌似是想把各种分类器都一下子讲到,然后有点前后照应的比较~真有意思,若是以前扔给我这种问题我肯定run一个logit regression就不管了,现在倒是有各种线性的、广义线性的、非线性的模型可以试着玩了,爽哎~
------------------
1. 自适应基函数模型
小小的复习一下上节课那个框架。
1. 数据。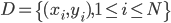
2. 模型。 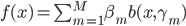 为基函数模型,其中
为基函数模型,其中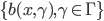 成为基函数集合。
成为基函数集合。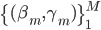 为参数。
为参数。
3. 损失函数(准则)。 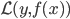 为损失函数,然后就转为一个优化问题:
为损失函数,然后就转为一个优化问题:
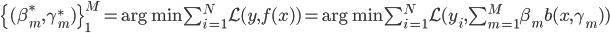
4. 算法。 前向分步算法。
- 初始化:
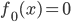
- 迭代:For m=1 to M,
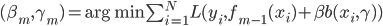
- 令
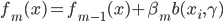 。
。 - 输出
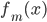 。
。
在此框架之下,除了上节课的Adaboost之外,还可以套用多种其他的基函数,然后1)定义损失函数 2)给出迭代那一步的优化算法,就可以实现一种boost提升算法了。
2. 应用回归问题
先采用均方误差的损失函数,定义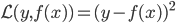 ,这样就可以得到
,这样就可以得到
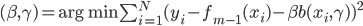
然后定义:
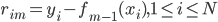 ,
,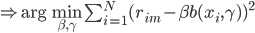 。这里
。这里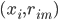 之后用回归树来求的话,就是梯度回归树算法。
之后用回归树来求的话,就是梯度回归树算法。
梯度回归树提升算法
- 初始化:
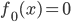
- 迭代:For m=1 to M,计算
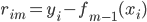 。由
。由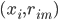 用回归树求得
用回归树求得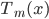 .
. - 令
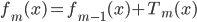 。
。 - 输出
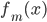 。
。
3. GTBA,梯度树提升算法
先吹捧一下:这个算法就是此书作者本人开发的,然后已经搞出来了软件包,可以做回归也可以做分类,貌似效果还胜过随机森林(当然是作者自己给出的那些例子...)。
损失函数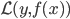 为可微的。
为可微的。
我们的优化目标是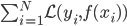 ,也就是说实际上我们不是直接对
,也就是说实际上我们不是直接对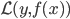 进行优化,而是仅仅在所有观测的数据点上优化,所以仅跟
进行优化,而是仅仅在所有观测的数据点上优化,所以仅跟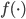 在这些观测点上的值有关。感觉这里就是说,我们使用有限的观测到的信息来推断一个连续的函数,然后类推并用于其他未观测到的点。
在这些观测点上的值有关。感觉这里就是说,我们使用有限的观测到的信息来推断一个连续的函数,然后类推并用于其他未观测到的点。
定义:
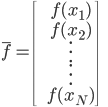 ,这样这个问题就从一个直接优化
,这样这个问题就从一个直接优化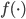 的泛函问题转化为一个优化多元函数的问题...而对于一个多元函数,我们可以直接用梯度下降法。定义梯度为:
的泛函问题转化为一个优化多元函数的问题...而对于一个多元函数,我们可以直接用梯度下降法。定义梯度为:
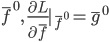 ,这样
,这样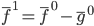 。类似的,我们可以定义
。类似的,我们可以定义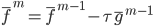 ,其中
,其中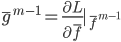 。累加起来,就是
。累加起来,就是
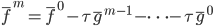 ,这里
,这里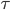 可以是常量也可以随着
可以是常量也可以随着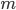 改变。
改变。
定义完梯度下降之后,就是GTBA算法了。
- 初始化。
- 迭代:For m=1 to M,计算
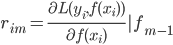 ,然后由
,然后由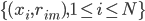 用回归树求得
用回归树求得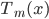 。
。 - 令
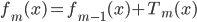 。
。 - 输出
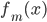 。
。
一些梳理
1. 参数。这里显然有如下参数需要设定:
- M:迭代次数。这是这个算法最主要的参数,需要用Cross-validation来算。
- J:树的大小。建议4-8,默认为6。
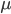 :收缩系数。
:收缩系数。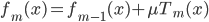 这里可以加上
这里可以加上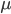 这个参数,决定收缩的速度,0-1之间。
这个参数,决定收缩的速度,0-1之间。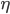 :次采样率,0-1直接,默认0.5。用于做subsampling。
:次采样率,0-1直接,默认0.5。用于做subsampling。
2. 特征变量评价
这个算法的一大优势就是可以给出各个自变量的评价。比如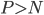 的时候我们可能面临特征变量选择问题。
的时候我们可能面临特征变量选择问题。
用t表示树中的节点,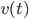 表示t节点所用的变量,
表示t节点所用的变量,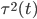 表示t节点产生的均方误差的减小值。之后定义:
表示t节点产生的均方误差的减小值。之后定义:
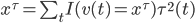 ,可用这个值来刻画变量的重要性,从而进行特征评价。
,可用这个值来刻画变量的重要性,从而进行特征评价。
3. 通用工具
该算法对于数据无特殊要求,有一批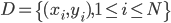 都可以扔进去试试,故可以作为其他算法的benchmark。
都可以扔进去试试,故可以作为其他算法的benchmark。
此外,从贝叶斯分类器的角度,我们要找的是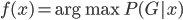 ,这样除了原有可以观测到的
,这样除了原有可以观测到的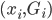 之上,还可以衍生出一个
之上,还可以衍生出一个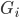 向量,即
向量,即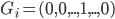 ,第k个位置为1如果观测到的
,第k个位置为1如果观测到的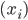 对应第k类。一下子就可以扩展整个数据集,也可以进一步对每类都赋一个概率,不单单是0-1这样。
对应第k类。一下子就可以扩展整个数据集,也可以进一步对每类都赋一个概率,不单单是0-1这样。
3 replies on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十五)”
我来火速沙发~~~
居然会讲随机森林。。。
多么经典的算法呀...怎么可能不讲呢?