前馈神经网,BP算法,AE(自编码器,Auto-Encoders)
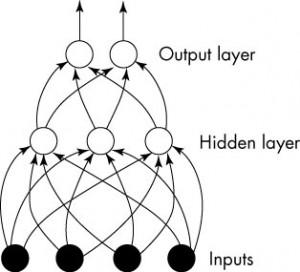
1. 前馈神经网(Multilayer Feedforward Network)
前馈神经网大致就是这个样子,一层一层的结构。这样,我们就由第一代的神经元系统繁殖出来了一个神经元群落...看起来很高深的样子。
先说一些参数和记号:
- L:网络的层次
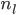 ,
,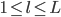 :表示第
:表示第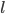 层中神经元的个数。特别的,
层中神经元的个数。特别的,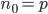 为所有输入变量的个数(x的维数),
为所有输入变量的个数(x的维数),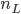 是网络输出的个数。
是网络输出的个数。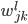 ,
,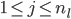 ,
,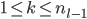 :相邻两层(
:相邻两层(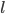 到
到 )之间的连接的权重。
)之间的连接的权重。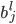 :第
:第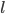 层第
层第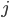 个神经元的偏置值。
个神经元的偏置值。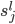 ,
,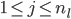 ,
,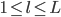 :第
:第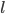 层第
层第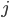 个神经元的状态值。
个神经元的状态值。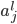 ,
,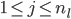 ,
,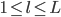 :第
:第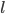 层第
层第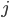 个神经元的活性(activation),或称为输出。
个神经元的活性(activation),或称为输出。
基本关系:
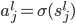
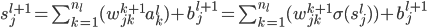 ,
,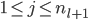 ,
,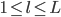
模型: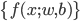 为
为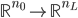 的映射。
的映射。
2. BP算法(网络学习/拟合)
给定数据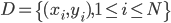 ,定义
,定义
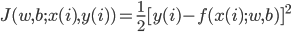
那么
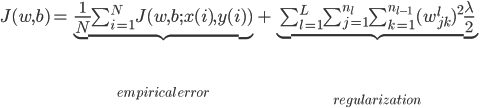
接下来的拟合优化问题就是最小化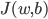 。这里可以采用梯度下降:
。这里可以采用梯度下降:
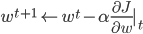 ,
,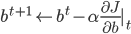 ,所以需要求得这两个梯度(偏导)项。
,所以需要求得这两个梯度(偏导)项。
定义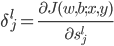 ,这样
,这样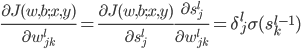 ,其中
,其中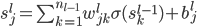 。
。
类似的,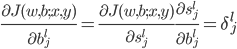
为了解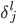 这个东西,我们需要后向递归。
这个东西,我们需要后向递归。
首先在第L层: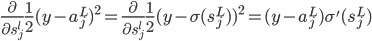 ,然后
,然后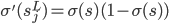
For L-1,...,1,我们有 ,这样就一直可以迭代反推至第一层。
,这样就一直可以迭代反推至第一层。
3. AE(自编码器,Auto-Encoders)
自编码器可以算是一个简化的神经网,大致只有三层:0,1,2。其中输入是x,输出也是x,但是中间进行了一个过滤。直观的讲,就像一个文件压缩了一下,又解压缩。中间压缩包的体积要比源文件小,但是信息却基本没有损失。
AE基本上想达到两个目标:
1. 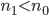 ,即中间那层的维数小于原始输入的维数p。
,即中间那层的维数小于原始输入的维数p。
2. 或者输出的均值非常小,即从第一层到最上面一层的输出较为稀疏,不是很强烈的关联。
下节课会讲到SVM。