照例继续本周笔记。这次我没啥废话了...
--------------笔记开始---------------
投影矩阵与消灭矩阵
首先是上次没证的若干OLS性质。基本都是公式。我就照抄原来econometrics做的笔记了。权当复习了...对计量有兴趣的、线性代数还不错的,建议去看《Microeconometrics- Methods and Applications》(?A. Colin Cameron / Pravin K. Trivedi )。
先定义两个矩阵,这两个矩阵会在某种程度上save your life while learning econometrics...投影矩阵和消灭矩阵。
复习一下,OLS估计量是 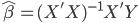 ,然后对应的Y估计量是
,然后对应的Y估计量是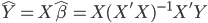 。所以,我们定义投影矩阵P为
。所以,我们定义投影矩阵P为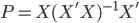 ,这样就有了
,这样就有了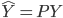 。也就是说,我们对Y进行了一次投影,然后得到了一个估计值。当然定义投影矩阵并不仅仅是写起来比那堆X简单,而是投影矩阵本身有着一系列良好的性质。
。也就是说,我们对Y进行了一次投影,然后得到了一个估计值。当然定义投影矩阵并不仅仅是写起来比那堆X简单,而是投影矩阵本身有着一系列良好的性质。
我们先来看把P投在X上会怎么样。显然,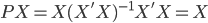 ,也就是说P不会改变X的值(本来就是把一个东西投到X上嘛~自己投自己怎么会有变化的嘛)。
,也就是说P不会改变X的值(本来就是把一个东西投到X上嘛~自己投自己怎么会有变化的嘛)。
然后呢,对P进行转置,则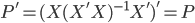 ,所以接下来
,所以接下来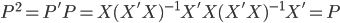 。
。
再定义消灭矩阵M。很简单,我们定义M为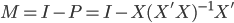 ,其中I为单位阵(对角线元素为1,其他为0)。这样M又有什么性质呢?显然
,其中I为单位阵(对角线元素为1,其他为0)。这样M又有什么性质呢?显然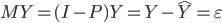 ,也就是说M对Y的效果是得到误差项。而与此同时,M对于X的作用就是
,也就是说M对Y的效果是得到误差项。而与此同时,M对于X的作用就是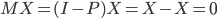 ,所以称为消灭矩阵嘛。继续,进行转置,则
,所以称为消灭矩阵嘛。继续,进行转置,则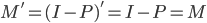 ,所以我们还有
,所以我们还有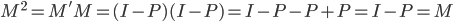 。
。
OLS估计值的方差
再次友情提醒,X不是随机变量,所以不要跟我纠结为什么没有条件期望公式之类的东西...
扰动项服从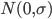 时,或者大样本下,OLS估计量的方差为:
时,或者大样本下,OLS估计量的方差为:
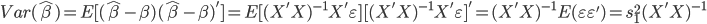
这里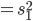 为样本方差,所以其分布为:
为样本方差,所以其分布为: 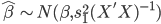 。这样一来,就有了一个t检验:
。这样一来,就有了一个t检验:
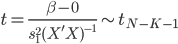 。
。
大样本下,就直接用正态检验好了。此外,如果我们进一步的有更多的同时检验的约束条件,那就是联合检验F。这个就不赘述了...
高斯-马尔可夫定理
顺便还证了一下高斯-马尔可夫定理...这个不像OLS,每次我可记不住他的证明,每次都是现翻书...
我就直接抄wiki了。
选择另外一个线性估计量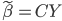 ,然后C可以写为
,然后C可以写为 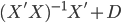 ,则D为k*n的非空矩阵。
,则D为k*n的非空矩阵。
那么这个估计量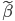 的期望是 :
的期望是 :

所以,为了保证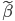 无偏,则必有
无偏,则必有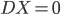 .
.
继续求方差:

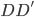 是一个半正定矩阵,
是一个半正定矩阵,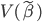 肯定要比
肯定要比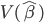 大~得证。
大~得证。
变量选择与收缩方法
为了降低测试误差(减少函数的复杂度),有时候会放弃无偏性而进行变量选择。这里首先就是Ridge OLS(岭回归)。还是算一下这个东西好了。
岭回归就是对估计量另外加一个约束条件,所以很自然的想到拉格朗日乘子法。ridge regression的目标函数为,
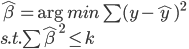
可以重写为
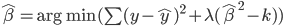
记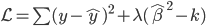
这样我们就得到两个一阶条件:
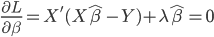 和
和 ,所以有:
,所以有:
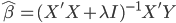
这里还可以看出,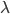 的取值都是对应
的取值都是对应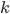 的。
的。
Lasso则是把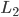 改成
改成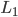 ,已经没有解析解了...
,已经没有解析解了...
至于为什么叫收缩方法,可以将X进行奇异值分解,然后可以得出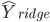 的方差将变小...我就不写证明了,感觉这一块儿讲的也不是很透彻。
的方差将变小...我就不写证明了,感觉这一块儿讲的也不是很透彻。
3 replies on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(四)”
能问一下为什么要保证估计的β无偏吗?
无偏?主要是大样本下保证估计值趋近真值....
shrink 也是把参数向0收缩