前言的废话:有种被统计学洗脑的感觉,跟搞统计的接触的有点太多了吧...哎,算了,难得有点感悟记录一下吧...喵。本文试图以一个典型的统计学的思维过程来叙述,呃,可能功力不足,凑合着看吧,也不枉我连续几天做梦都是直方图 密度曲线 average treatment effect之类的。
-------------------------------------------废话结束了-----------------------------------
Variance这个词很好玩,如果是用在统计的情境中就中文译作方差,公式就是 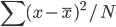 ,写成列向量(N*1矩阵)的形式就是
,写成列向量(N*1矩阵)的形式就是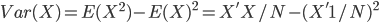 ,1这里是N×1个1的列向量。从公式的形式就可以看出是一个二阶中心距,即距离中心的距离的平方(二阶)和。然后既然是二阶距,那么自然的衡量的就是某个数据集分布的离散情况。越大越散,越小越密。此为一维(这里指只有一个观测维度的情形)相信这样的定义实在是太耳熟能详了。方差有个小弟叫做标准差,就是方差开平方。这个也没啥说的,有意思的是大家习惯用字母
,1这里是N×1个1的列向量。从公式的形式就可以看出是一个二阶中心距,即距离中心的距离的平方(二阶)和。然后既然是二阶距,那么自然的衡量的就是某个数据集分布的离散情况。越大越散,越小越密。此为一维(这里指只有一个观测维度的情形)相信这样的定义实在是太耳熟能详了。方差有个小弟叫做标准差,就是方差开平方。这个也没啥说的,有意思的是大家习惯用字母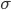 来标注他,于是有了著名的六-西格玛原理...好吧,其实最有用的就是正态分布的几个西格玛了(随便偷张图):
来标注他,于是有了著名的六-西格玛原理...好吧,其实最有用的就是正态分布的几个西格玛了(随便偷张图):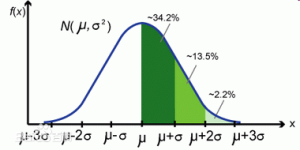
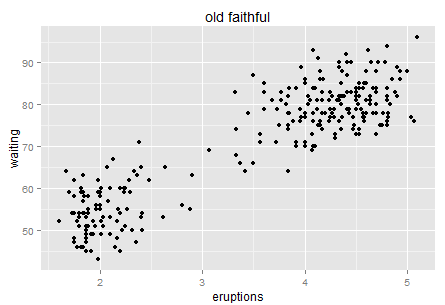
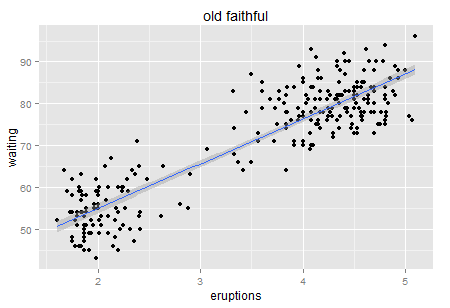
然后我们看简单的二维。二维就是散点图,没什么特别说的。找张著名的散点图来(随便找的,懒得自己去R里面画了。最后还是乖乖的去R里面的画了,还是自己画的好用一些,果然偷懒不容易,唉,我写博客实在是太敬业了!)。
背景知识大家可以去自己搜搜,反正就是黄石公园某个自然形成的间歇性喷泉,每次喷发的时间和等待时间的散点图。挺简单的对吧。这个数据点也不多,大家一眼扫过去大概百余个的样子。可是这幅图真的很有意思,跟Variance的联系实在是太紧密了。
我们先来说直觉。如果让你用自然语言(而非统计或者数学公式)来讲述这个图,比如你带这你刚上小学的孩子去黄石公园玩,他好奇的在等待这个喷泉喷发,这个时候你应该怎么跟他讲?嗯,可以大概说一下,“你看基本上呢,你等的时间越久,下一次喷发的时间就越长哦。让我们一起来计时~” 然后小朋友看了一眼图,不服的说到,“什么嘛,明明是等了如果超过一小时(或70分钟),那么下一次基本上喷发时间才会长(4-5分钟)。”。那么到底哪种说法更准确呢?
(吐槽君:自从上次写了乐高机器人之后,落园的段子里面的科普对象就从同学们降低到小朋友了,喵~)
好啦,不跟小朋友玩了,我们得研究一下更fancy一点的方法。说白了就是,用一个什么样的模型可以让经过我们模型处理的Variance尽量的小呢?
嗯,同学们说试试回归呗,明显的正相关性啊。你都说了啊,X的增加Y也在增加(先不要理会因果即X和Y谁先谁后,我们只说相关)。
所以我们虽然得到了一个显著的正相关关系,但是回归模型的R方只有81%(当然已经很好了,只是我们希望更好嘛)。来看看对应的残差分布:
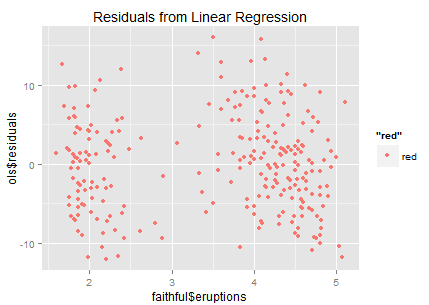 残差好像挺散的(最理想的残差就是白噪音了,说明没有任何信息量了),但是隐隐约约也能看出来有两群这样。于是很自然的,有同学说,我们去试试聚类啊。
残差好像挺散的(最理想的残差就是白噪音了,说明没有任何信息量了),但是隐隐约约也能看出来有两群这样。于是很自然的,有同学说,我们去试试聚类啊。
在去试聚类以前,先说说大名鼎鼎的K-mean算法的一些基石。
上面不是罗嗦了一堆variance在一维情形下的定义嘛,那么推广到二维,也很简单。
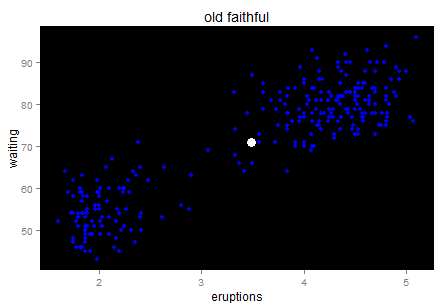
定义二维的中心点: 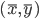 ,然后就可以定义二维方差: 每个点到图中心的距离的平方和。看图就知道了。
,然后就可以定义二维方差: 每个点到图中心的距离的平方和。看图就知道了。
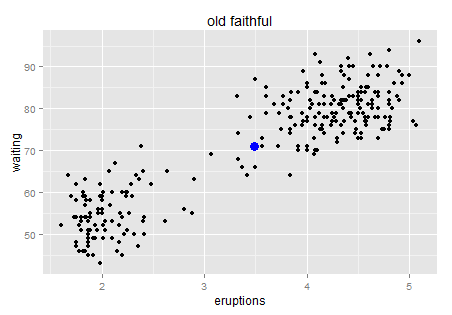 蓝色的就是中心点。这里我们就不罗嗦什么均值容易受极值影响之类的了,那些也是看菜下料的,我们的数据看起来还好。(突然间为什么有种牛郎织女鹊桥相会的即视感...原来古人观星也是有异曲同工之妙呀,天空就是一个大大的散点图——勿喷,我保证下面不跑题了)
蓝色的就是中心点。这里我们就不罗嗦什么均值容易受极值影响之类的了,那些也是看菜下料的,我们的数据看起来还好。(突然间为什么有种牛郎织女鹊桥相会的即视感...原来古人观星也是有异曲同工之妙呀,天空就是一个大大的散点图——勿喷,我保证下面不跑题了)
对于一个线性回归模型来讲,我们看的就是残差项的方差——残差项方差越大,表示他们分布的越散,那模型捕捉到的信息就少。
对于聚类呢,也可以看相应的方差:每个类里面的点到类中心的距离平方和 -> K-means。K-means虽然是通过迭代来实现的,但他的原理大致也是让二维的二阶中心距最小(由每一次迭代的损失函数来决定)。一眼扫过去大概可以分成牛郎织女两堆星星,那么我们就聚两类好了。显然不用跑程序我们也知道,聚成两类之后的组内方差和肯定比直接跟中心点算一个方差要小。
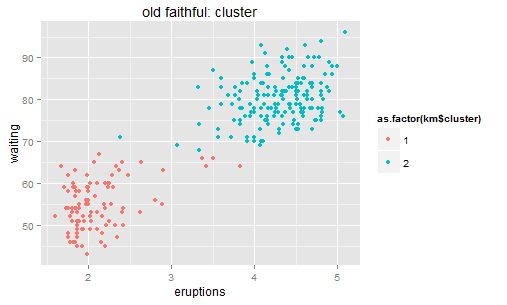 聚成两类之后呢,我们类似定义的残差就是两类中每个点距离其中心点的Y轴距离(因为会直接把中心点作为每类的预测值)。还是画个残差图看看。
聚成两类之后呢,我们类似定义的残差就是两类中每个点距离其中心点的Y轴距离(因为会直接把中心点作为每类的预测值)。还是画个残差图看看。
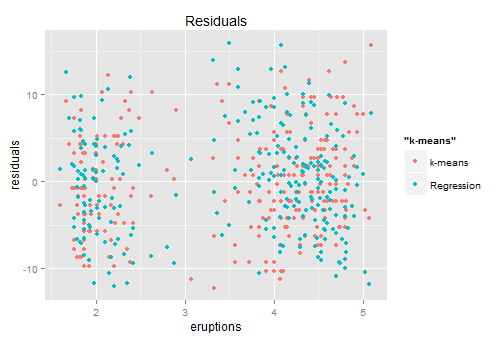 红色是K-MEANS给出的残差,蓝色是回归给出的残差。貌似这两个长得还是挺像的,也是左右两群,虽然每群中两者长得都不太一样...这个时候我们就可以回到和小朋友的对话了:你们说的都有道理,都有8成的准确率,谁也没比谁更好很多。
红色是K-MEANS给出的残差,蓝色是回归给出的残差。貌似这两个长得还是挺像的,也是左右两群,虽然每群中两者长得都不太一样...这个时候我们就可以回到和小朋友的对话了:你们说的都有道理,都有8成的准确率,谁也没比谁更好很多。
于是我们尝试在每组内再做回归?会有效果么?
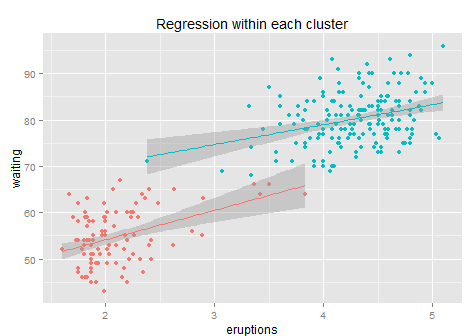 见效寥寥...引入聚类后回归模型的R方从81%升到了84%,才3个百分点。这主要是在每一类里面,我们很难找到残差的规律了,所以这样只是通过组别信息的增加减少了组间方差,而其实从上图我们也可以看出每个组内的残差方差还是很大的、每条回归拟合线的斜率从最初的10降低到6和4,每个子回归的R方只有10%不到,能给予的信息已经很少了,所以整体模型只是增加了一点点准确性。但是无论如何也比直接玩回归的效果要好(之所以用k-means而不是简单粗暴的用类似x>3.5这样来分成两类,是因为k-means是按照其损失函数优化过的、给出的是最优的两类聚类结果)。
见效寥寥...引入聚类后回归模型的R方从81%升到了84%,才3个百分点。这主要是在每一类里面,我们很难找到残差的规律了,所以这样只是通过组别信息的增加减少了组间方差,而其实从上图我们也可以看出每个组内的残差方差还是很大的、每条回归拟合线的斜率从最初的10降低到6和4,每个子回归的R方只有10%不到,能给予的信息已经很少了,所以整体模型只是增加了一点点准确性。但是无论如何也比直接玩回归的效果要好(之所以用k-means而不是简单粗暴的用类似x>3.5这样来分成两类,是因为k-means是按照其损失函数优化过的、给出的是最优的两类聚类结果)。
问题来了,为什么我只聚成两类而不是三类五类甚至更多呢?主要是怕过拟合,数据才200多个点,聚太多的话很容易过拟合了。大数据的情况下可以尝试其他办法。
好了,废话了这么多,其实统计学家们已经不仅仅玩这些了。其实我们上面的残差图传达了一个很重要的信息就是残差的分布不是一个白噪声(或者说不是均值为0、方差为常数的正态分布),称之为异方差(Heteroscedasticity)。异方差有很多很多情形,最简单的就是随着X的增加而增加。还是网上随便找了个图:
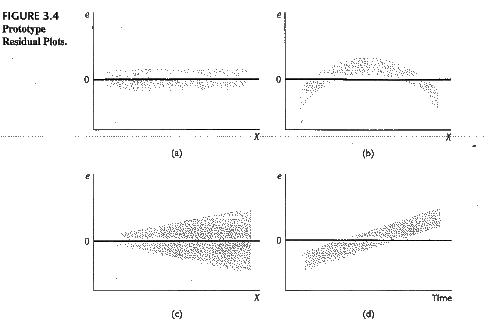 异方差的存在使得我们模型的估计(或者基于训练数据预测)精度有限(先不考虑validate- test那些),所以统计建模常年在跟残差项的分布作斗争——反正看到你有什么规律,我就可以提取出来更多的信息放到我的模型中。计量经济学家喜欢说残差项是垃圾桶,但其实也是金矿——没办法呀,资源有限,不能太浪费。
异方差的存在使得我们模型的估计(或者基于训练数据预测)精度有限(先不考虑validate- test那些),所以统计建模常年在跟残差项的分布作斗争——反正看到你有什么规律,我就可以提取出来更多的信息放到我的模型中。计量经济学家喜欢说残差项是垃圾桶,但其实也是金矿——没办法呀,资源有限,不能太浪费。
然后是一些补充的废话时间。
残差和模型:只要模型可以做预测,那么残差就是存在的,跟模型是线性还是树形之类无关。残差的定义仅仅是真实的y减去预测的y(基于train数据)。
残差和损失函数:对于最小二乘法来说,迭代解数值解的话,损失函数就是残差平方和了(截距项的存在保证残差的均值为0,所以等同于残差的方差)。同理,大部分机器学习算法的损失函数都跟残差项相关,用到二阶的话基本就是在最小化残差的方差。从这个角度而言,统计建模都是在跟残差作斗争。这里和专注于因果推断的计量经济学家就很不同了——前几年大家炒得火热的trade off between consistency and efficiency就大约来自各自的坚持。
残差、频率派与贝叶斯派:上面说的其实更多是频率派的东西,我好像没提过什么 posterior 之类的对吧。不过从我的理解来看上述的分析在贝叶斯的框架下很多也是等价的,所以这个不牵扯。下面说的有频率也有贝叶斯派(的观点),大家凑活着理解吧。
残差、异方差和稳健标准误:上面说了异方差是我们又爱又恨的——异方差说明我们的模型不够好,但是如果能看到异方差规律的话也给我们进一步改进的机会。在上个世纪为了大约的减少异方差的影响,就出来了一个稳健标准误(robust standard error)的概念——Heteroscedasticity-consistent standard errors,最著名的就是Eicker–Huber–White了。Eicker–Huber–White主要是改变了三明治矩阵那儿——常用R里面sandwich()之类的话不会陌生,有肉有面包。Eicker–Huber–White简单的说就是用残差的估计值放进去改变meat(普通最小二乘法假设meat那里有个常量),以期系数估计值的方差会少受影响。但是吧,Eicker–Huber–White的问题就是没有试图去进一步分析残差里面可能的patterns...所谓的广义最小二乘、可行广义最小二乘(FGLS)之类的,同理,试图去找到一个残差简单的线性或者非线性的规律,然后改进模型中从而减小残差的方差)。另一类有意思的Eicker–Huber–White就是引入聚类的概念——在每一类中残差为白噪音,类别间允许异方差,称之为cluster robust standard error,只是大家记得啊cluster的数量趋近于无穷的时候这货才是consistent的,不要像我一样忘了这个假设...
残差项和降维:一般说来,引入的跟Y相关的维度越多,残差含有的噪音就会越小。但是出于过拟合的考虑,我们需要降维(加入regularization即可)。此外很多时候模型的目的不仅仅是预测,而是提取显著特征,那么对于特征的选择也是需要从模型的角度最大化信息量(比如AIC或者BIC准则,或者直接regularization看惩罚增加的时候各个X的衰减速度,然后选择一个惩罚程度对应的特征估计值,但这里并不一定是validate给出的最优惩罚程度,目的不一样嘛)。
残差和实验数据分析:异方差的存在不会影响我们对于average treatment effect估计的一致性——一致性是从实验设计的随机划分来的,跟估计精度无关。可是大家对于简单的实验组对照组的对比越来越不满,尤其是在实验对象很多而且彼此之间异质性很强的情况下,单单一个ATE给出的平均意义上的效果已经满足不了大家的胃口了。于是大家有了heterogenous treatment effect这个说法——实验效果本身也是异质的。简单的来说,如果除了随机分组之外我们还能观测到另外一个维度(称之为控制变量或者covariates),那么分位数回归(quantile regression)就可以给出随着那个维度的变化实验效果的变化。可是维度很多的时候呢?先降维?
说了这么久,看到heterogenous第一反应显然应该是variance啊,要不拿什么来衡量heterogenous呢?不过其实吧,我是想说,有一类很好玩的paper就是试图看我们还能不能从treatment effect里面找到比ATE更多的信息量。比如下面这篇:
Ding, P., Feller, A., and Miratrix, L. W. (2015+). Randomization Inference for Treatment Effect Variation. http://t.cn/RzTsAnl
好吧,到此为止吧,已经越来越学术了...本来就是随便记点东西的。
哦,还有code...懒得保存R了,直接贴过来吧。
library(ggplot2)
data(faithful)
names(faithful)
#scatter plot
ggplot(data=faithful, aes(x=eruptions, y =waiting)) +geom_point()+ggtitle("old faithful")
#scatter plot with regression line
ggplot(data=faithful, aes(x=eruptions, y =waiting)) +geom_point()+ggtitle("old faithful") + stat_smooth(method="lm")
#lm residuals
ols = lm(waiting~eruptions, data =faithful)
qplot(y=ols$residuals, x = faithful$eruptions, color="red")+ggtitle("Residuals from Linear Regression")
summary(ols)
###dark sky...
ggplot(data=faithful, aes(x=eruptions, y =waiting)) +
geom_point(color="blue",alpha=0.9)+ggtitle("old faithful")+
geom_point(aes(x = mean(faithful$eruptions), y = mean(faithful$waiting)), size = 4 ,color="white", data = NULL)+
theme(panel.background =element_rect(fill ="black",size = NULL),
panel.grid.major=element_blank(),
panel.grid.minor=element_blank()
)
###clustering
km = kmeans(faithful,2)
ggplot(data=faithful, aes(x=eruptions, y =waiting)) +
geom_point(aes(color=as.factor(km$cluster)))+ggtitle("old faithful: cluster")
km$centers
faithful_km = cbind(faithful,cluster = km$cluster)
centers = cbind(as.data.frame(km$centers) , cluster = 1:2)
faithful_km = merge(faithful_km, centers, by = "cluster",suffixes = c("",".center"))
faithful_km$residuals = with(faithful_km, (waiting-waiting.center))
##residuals comparison
library("gridExtra")
grid.arrange(
ggplot()+
geom_point(data = faithful_km, aes(x = eruptions, y = residuals,color = "k-means")) +
ggtitle("Residuals") +
geom_point(aes(y=ols$residuals, x = faithful$eruptions, color="Regression"),data =NULL)
)
###
lm2 = lm(waiting~eruptions+as.factor(cluster), data = faithful_km)
summary(lm2)
ggplot(data =faithful_km , aes(x=eruptions, y=waiting,color = as.factor(cluster)) )+
geom_point()+
stat_smooth(method="lm",data = subset(faithful_km, cluster ==1))+
stat_smooth(method="lm",data = subset(faithful_km, cluster ==2))+
ggtitle("Regression within each cluster")
#residuals
qplot(x=faithful_km$eruptions,y=lm2$residuals,color="red")
#within each cluster...lm's performance
lm3 = lm(waiting~eruptions, data = faithful_km, subset=cluster==1)
summary(lm3)
lm4 = lm(waiting~eruptions, data = faithful_km, subset=cluster==2)
summary(lm4)
#play time
faithful_km$c2 = faithful_km$eruptions>3.5
lm5 = lm(waiting~eruptions+c2, data = faithful_km)
summary(lm5)
11 replies on “从Variance说起:回归、聚类、残差和方差”
不错。精神病人思维广
[…] is the translation of my recent post in Chinese. I was trying to talk in the way that a statistician would use after having stayed along with so […]
关注落园5年了,抽空就来看看有没有更新,过来读读。
话说上一篇关于最小二乘君的博客,被xie大人赞为年度最佳,感觉这篇也不逊色
feedly受到xie大人博客破天荒更新,才知道这篇博客是双语版。。。
[…] Liyun Chen ’11 (Economics) is Senior Analyst for Data Science at eBay in Shanghai, China. The following post originally appeared on her economics blog in English and in Chinese. […]
哈哈。。。我还是在纠结clustering analysis 和 PLS, PCA 的关系。是上下层?你的代码是C++ 的?有matlab 的吗。。。求教~~~
博主说了代码是R的呀