众所周知,泰勒展开是数学分析和复变函数幂级数这一章最重要的公式。在复数域内更是任何一个解析函数都有泰勒展开式,这一下子就大大拓宽了函数的范围。
而后在复变有关于泰勒展开的唯一性证明。如果存在数列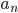 使得
使得
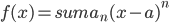 则
则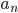 必是唯一的。
必是唯一的。
我们用的教材上证的时候是逐阶求导,个人觉得有些麻烦。其实很简单的一种道理就是因为x的n次幂(n=1,2,...)线性无关,所以若存在数列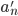 也满足该式,则两式相减可得
也满足该式,则两式相减可得 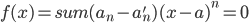 。由(x-a)的各次幂线性无关,则可知必有
。由(x-a)的各次幂线性无关,则可知必有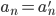 。因此唯一性得证。
。因此唯一性得证。
当时上课给老师说的时候,老师主要提出了两个问题:
1.有限维能不能推广到无线维
可能有限到无限在很多时候是难以直接推广的,但是这里应该没有问题,因为无论如何各项都是一一对应的。
2.函数线性无关怎么证明
其实函数的线性无关指的是在某一定义域内两函数的线性关系不随着其自变量x的取值而改变。因此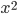 和
和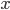 一定会是线性无关的。再由数学归纳法,可证。当然老师当时还提出可以使用范特蒙德行列式证明,确实是数学之间都是相通的啊!
一定会是线性无关的。再由数学归纳法,可证。当然老师当时还提出可以使用范特蒙德行列式证明,确实是数学之间都是相通的啊!
综上,大致写写这些思路,觉得复变函数确实是能开拓一下眼界的,还有泛函里面一些关于基坐标的定义,看来远远不是无源之水啊!
(忽然发现不知怎么将本文归类了……貌似没有数学这一类……读书有感吧!虽说读的是课本。)
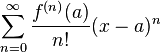
50 replies on “利用线性无关证泰勒展开唯一性的一点思路”
那些线性相关、线性无关的定义本来就没涉及维数,这个思路应该可以的。另外函数线性无关可以考虑用朗斯基行列式。
我最近在看泛函分析,觉得归到线性泛函挺合适的。我也去试试能不能把这个证明写出来。
Thank you very much!
不愧是学数学的,一看这答案就有深度。
我也是一边学泛函一边学复变想起来的……但是我泛函学的实在是太烂了……现在有专家在,我就不班门弄斧了~加油!
话说,真难得这篇日志也有人在关心~感动中,很多人对类似的日志大都直接自动屏蔽了……
证明可能还是存在不小的问题:从有限到无穷的的过程中.
本来觉得那些很显然的,但写了之后才发觉不对,真的是越显然的东西越难证明.
文档我放在 http://code.google.com/p/viewscode/downloads/list
你的文章中我看最认真的就是数学和 LaTeX(虽然已经转向ConTeX),而经济学和网站建设的我就不懂了就只能看看。其它的现在大家都是学生,有些东西是相似的也就不多说了。那个证明的我现在去问一下我的老师,看他怎么说。
我用的书复变函数是路见可的(上学期已经学过了),泛函分析是江泽坚的(这个就是我的毕业论文的方向了,学校没开这个课,只能自学)内容都不是很深(虽然我已经感到很困难了,但老师是这么说的)。而路见可的很多东西都没细讲。
你用的书是谁写的?
我的复变是钟玉泉的,泛函是山大版的郭大钧写的(自产自销,汗!不过感觉比rudin那本难一些……)
先谢谢你这么认真的看我的文章,感动ing~
不过泛函我们这边数学院的是本科就开啊,不知道你是哪里的?
另,有限到无限的问题,我依旧觉得最好的避免方法就是用数学归纳法,这样推广起来说服力比较大。个人愚见,不知合不合适……
确实用数学归纳法比较好说明,在 QQ 上问了老师但到现在还没回复我(他今年去进修了,不在学校),晚上应该会回我的,先看他怎么说再去修改。
是那两本《实变函数与泛函分析》吗?如果是《非线性泛函分析》就太难了(对我而言)。Rudin 那本前几天刚买来了,对我来说那本已经够难的了。我还是先用江泽坚的那本先入门再说。
我们学校自产自销多了,像数学书除了数学系其余的都是用自己学校老师写的书(高数有少数几个专业是用同济版的)
钟玉泉的复变函数,照老师的说法那本书建立在高数的上的,不过我没认真看过不了解。其实我们只教最基础的:解析函数基础、复积分、解析函数的级数理论和留数。
而路见可的书在解析函数的单值化问题上感觉根本没讲清楚个人感觉还是余家荣的在这块写的比较好(后面的同伦概念、柯西定理也是),不过书也都有各自的优缺点吧,看个人了。
是那两本一套的实变和泛函。其他的书我就不知道了。
对复变我没啥感觉,只是老师讲讲能听明白就满足了,毕竟不是数学专业的~
福建农林大学(真不知道当时报自愿的时候选数学怎么会跑到农大去)。学校数学类的课开得很少,专业选修课的几乎是经济和计算机的(除了大四的上点集拓扑)想多选一些数学的而没报那些选修课差点就因为学分不够要延期毕业了。
下午在ctex跟LiYanrui(李延瑞)版主测试他写的ConTeXt MkIV 中文标点处理模块(什么也做不了,就是做小白鼠了),现在才看到,奇怪了这几次有回复的时候都没邮件提醒了。
我不知道是不是服务器出问题了,最近网站不太稳定。麻烦你多来踩几下了。
难得有数学院开其他课比本专业多。我们这边数学院全是数学课……恐怖。
刚上来,就收到回信
鸿 2009-11-29 18:49:32
证明可以
最后用内积的方法与区间[a,b]有关,与函数f的定义域要求不符,不能用
看来最后那个不行,而前面那些也只是没有原则上的错误。细节上还是要修改,只是现在时间不够了还有其它的要做(文档还是放在那里),等有时间我会把这个证明写得更完善一些(把你说的用数学归纳法的也写上)。
恩,我觉得没必要用内积空间Hilbert,简单的只把它看作一个无线维的线性泛函可能会避免一些争议。
话说,线性无关和正交之间是什么关系?线性无关的一定正交么?
正交的向量一定是线性无关,线性无关不一定正交,但一组线性无关的向量可以通过 Gram-Schmidt 正交化得到一组正交的向量它们之间可以唯一的相互线性表出。
这些你应该也知道真是多余了。
全是数学课?我们学校怎么不那样呢?
看来真是哪里出问题了,都没有邮件提示,自己经常来看看了。
没有邮件提示?我自己倒是能收到。测试一下~
还是没有啊,刚才去看了一下邮箱,我最后一次收到提示说11月6日
你这里有设置不再提示之类的吗?在其它博客我看到过,如果有可能是什么时候我误选了。
不知道,我在调插件,我记得以前邮件通知是没有问题的。
刚才的一个有收到了。
恩,貌似没问题了。
p.s. 你可以扫一眼垃圾邮件……
嘿嘿,顺道把留言通知的正文改了改。看看现在能收到不?
真是不好意思,我现在才想起来上次创建过滤器
的时候设置错了,把那个过滤器删了就好了。
另,正交的那个问题……你原谅我的记忆力吧,线性代数的施密特正交化都忘光光了。该打!
设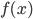 有泰勒展开式
有泰勒展开式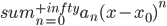 与
与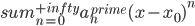 .
.
从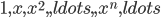 中任取
中任取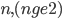 个,按照
个,按照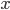 的升幂排列后得
的升幂排列后得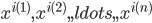
设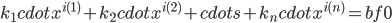 ,则
,则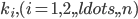 当不全为
当不全为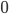 时,
时,
由代数基本定理可知在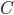 上至多有个
上至多有个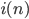 互不相等的
互不相等的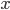 使等式成立.
使等式成立.
所以只有当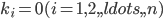 时该式恒成立,所以
时该式恒成立,所以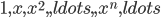 是线性无关的.
是线性无关的.
由前面假设有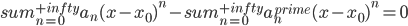 ,由前面证明可得
,由前面证明可得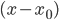 的各次幂线性无关,则可知
的各次幂线性无关,则可知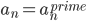 .
.
至于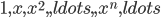 是线性无关的用数学归纳法证明,我试了几次都失败了.
是线性无关的用数学归纳法证明,我试了几次都失败了.
才想起来你这边是支持TeX代码的,直接写这边更方便.
现在不支持 TeX 代码?
现在好了……支持是支持,不过要用两个$括起来公式,而不是一个。要不美元符号怎么打,呵呵。我帮你改了一下,就好了。
过几天整理出来一个反证法证明给你看看哈。
要两个$ 之前我还因为两个$是行间公式。(你上次都说了,都是我没看清)
本来还想从朗斯基行列式继续做下去(也才发现之前我竟然把行列式写成了矩阵),后面发现还是从有限到无穷的过程不好说明,最后找到一组无穷个向量线性无关的等价定义:其任意有限子集是线性无关的。
用反证法?想不出来,看你的证明了。(后来看了你的简历,才发现你学的数学课并不比我少,佩服啊)
没,我的思路很简单,只是最近没有整块的时间写出来而已。
你看我的简历要留心的是,哪些是已经学完的,哪些是being studied的。呵呵。
看到第二届R会议了……我有注意哪些已经学完的
我已经学的:数分,高代,近代,解几,概率与数理统计,复变函数,离散数学(这个应该不算才对)所以很惭愧啊,之前也遇到过让我汗颜的女生(比我强的很多,但很少能让我发自内心的佩服),也不是学数学的(尤其在代数方面)。
后来想起上学期老师讲课时的证明也不是用逐点求导。这里的公式效果不好(WordPress 官方的很不错)用图片了(ConTeXt 和 LaTeX 的公式对齐环境等代码有所不同,就不去修改放在这里了)
又写错了:逐次求导 (老犯这种错误)
你可以直接用img标签插入图片,呵呵。
你说的WP官网效果是指?给个地址吧!
汗~~!完全不会 HTML/XHTML……
一时间也找不到有写公式的博客,这是我上次在那里做测试用的
测试
还是打错字了,无视它吧(上次在谢益辉那边留言也是,明明检查过了,真不像学数学的)
帮你改过来了,没事儿,呵呵。
fine. I think you are using another plugin...
I'll change later on, since I need some tests.
那里默认就支持 TeX 了(想找一个支持 TeX 的免费博客),只是那里虽然支持,但其它方面却不尽人意,稍微定制一下就要收费(连修改默认字号行距也要)
换一个在线公式的服务器可能效果就会好很多,我试试
sitmo
mathtran
sitmo
mathtran
希望这次没用错 img 标签
嗯?莫不是我禁掉了img标签?没事没事,你把地址直接放上来,我看到后编辑一下就好
我在其它地方试过了都可以的在这里就不行了,不会 img 标签只能给个链接了。
Using LaTeX in WordPress"
我觉得上面那那个的效果比你现在用的这个好
嗯,我改过来了。顺便测试一下。
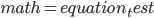
就是 Using LaTeX in WordPress 里面介绍的


用好像不行(还是我用错了?)
我在这里用
不行,正确的要怎么用?你随便留就好,我能看明白就直接在后台编辑。
所有用错的标签都没了,想用 code 标签插入 我所写的 img标签 也不行。
恩,估计是WP默认有过滤html标签。
第一次看到有人在 blog 回复里交流数学问题。我个看到数学公式就晕
嗯……见多了就不奇怪了……
让大家见笑了,用相同的内容在这里问数学问题,在 CTeX 问排版问题