1. SVM优化问题
1) 原问题
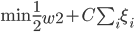
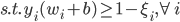
2) 拉格朗日形式的表述
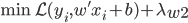
其中,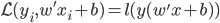 。
。
3) 对偶问题
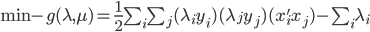
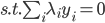
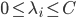
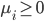
4) SVM分类器
(i) 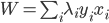
(ii) 选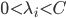 ,
,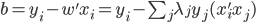 ,然后
,然后 。
。
(iii)SVM分类器 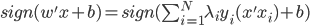
2. SMO算法
1) 基本思想:迭代下降、坐标下降
一次要选择两个变量(否则会破坏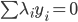 的约束),之后就可以解这个双变量优化问题。
的约束),之后就可以解这个双变量优化问题。
2) 两个变量的优化
任取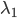 ,
,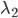 作为变量,其他
作为变量,其他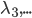 作为常量。
作为常量。
展开的矩阵大致如下:

目标函数=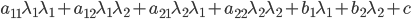
这样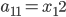 ,
,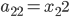 ,
,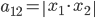 ,
,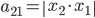 。
。
约束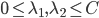 (对应对偶问题)
(对应对偶问题)
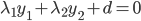 ,这里d代表其余不改变的那些
,这里d代表其余不改变的那些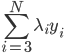 。
。
化到单变量的话,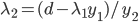
所以,
- 目标函数=
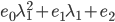 ,最优条件
,最优条件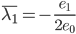
- 约束
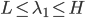 ,其中
,其中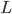 和
和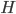 分别为lower/upper bound。故必有最优点在L、H之间或者L、H之一。
分别为lower/upper bound。故必有最优点在L、H之间或者L、H之一。 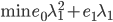 ,
,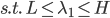 ,可以解得
,可以解得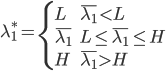
这里虽然需要迭代很多次,但是迭代的每一步都比较快。
至于如何选择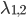 ,第一个变量
,第一个变量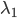 可以选择
可以选择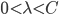 ,同时
,同时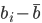 最大。第二个变量选择
最大。第二个变量选择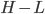 最大的。
最大的。