这节课主要是讲线性优化的对偶问题。感觉这东西貌似在运筹学的时候被折腾过一遍,现在又来了-_-||
附赠个老的掉牙的段子...
有人问经济学家一个数学问题,经济学家表示不会解...
然后那个人把这个数学问题转成了一个等价的最优化问题,经济学家立马就解出来了...
好吧,我还是乖乖的赘述一遍对偶问题吧,表示被各种经济学最优化问题折磨过的孩子这点儿真是不在话下。
--------------------------------------------------------------------
1. 对偶问题的一般情况
1) 优化问题
一个典型的最优化问题形如:
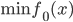
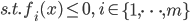 (不等式约束)
(不等式约束)
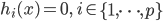 (等式约束)
(等式约束)
2) 优化问题的Lagrange (拉格朗日)函数
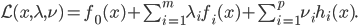
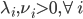
3) 对偶函数
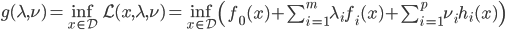 称为该优化问题的对偶函数。此时,
称为该优化问题的对偶函数。此时,
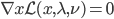 ,显然这个时候一阶偏导数为0。
,显然这个时候一阶偏导数为0。
4) 对偶问题
我们称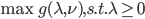 为原优化问题的对偶问题,可化为最优化问题的标准形式
为原优化问题的对偶问题,可化为最优化问题的标准形式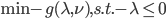 。
。
如果原优化问题为凸优化,则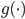 必为凹函数,从而最终的标准形式依旧是一个凸优化问题。
必为凹函数,从而最终的标准形式依旧是一个凸优化问题。
5) 弱对偶性
令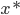 为原问题的解,则
为原问题的解,则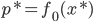 ,且
,且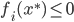 ,
,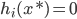 .
.
令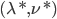 为对偶问题的解,则
为对偶问题的解,则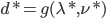 ;
; 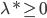 .
.
定理(弱对偶性):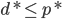 ,即对偶问题的优化值必然小于等于原问题优化值。
,即对偶问题的优化值必然小于等于原问题优化值。
6) 强对偶性
当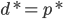 时,两者具有强对偶性;满足该条件的称之为constraint qualifications,如Sliter定理。
时,两者具有强对偶性;满足该条件的称之为constraint qualifications,如Sliter定理。
强对偶性满足的时候,原优化问题就可以化为一个二步优化问题了。
7) KTT条件(库恩-塔克条件)
局部最优化成立的必要条件:
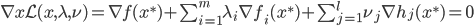 (一阶条件)
(一阶条件)
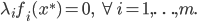
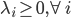
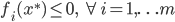
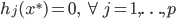
注:SVM满足强对偶性,所以可以直接解对偶问题。
2. 对偶问题应用于SVM
1) SVM的最优化问题
上节课可知,SVM的最优化问题为:
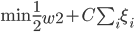
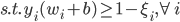
写成标准形式就是
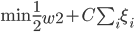
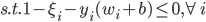
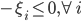
这样这里总计有2N个约束条件。
对应的Lagrange函数为:
这样一阶条件就是
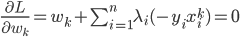
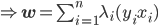
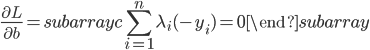
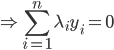
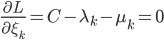
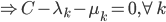
这样最后我们有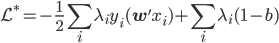 .
.
3) 对偶函数
这里的对偶函数就是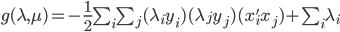
4) 对偶问题
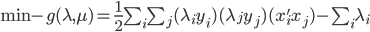
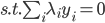
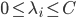
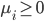
5) KKT条件
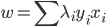
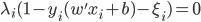
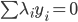
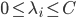
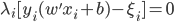
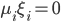
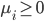
6) SVM分类器
- 解对偶问题,得到
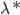 ,
, 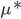
- 计算
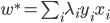
- 计算
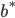 :找到一个
:找到一个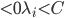 (非边界上),从而满足
(非边界上),从而满足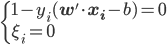 。由
。由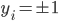 ,我们可得
,我们可得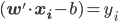

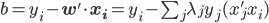
- 平面分类器:
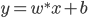 ,
, 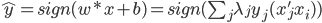 ,故只与内积有关。
,故只与内积有关。
这样下节课就会讲到解对偶问题的方法,以及SVM和kernel methods的联系。
8 replies on “统计学习精要(The Elements of Statistical Learning)课堂笔记(二十):SVM”
看课堂笔记还附带笑话的,表示笑话看到笑点了,数学公式严重地表示不能理解。
这课的内容不是老教授上的吧,如果是的话,真心给跪了。突然想起,要么还有助教这一角色的存在?
是老教授上的呀,吴老师可是数学出身。
库恩塔克条件你没听过?不会吧...这个跟ml没啥关系,就是一个全局最优解呀。
有几个问题,
1.拉格朗日函数中vi为什么要大于0?
2.对偶函数中的inf是求无穷大还是无穷小还是别的啊
1.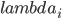 ?这个是库恩塔克条件规定的...因为已经都化为标准形式了所以这里一定要求大于0。见: https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions
?这个是库恩塔克条件规定的...因为已经都化为标准形式了所以这里一定要求大于0。见: https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions
2. inf是最小下界(下确界)吧...有点类似于min,但不要求一定达到。见: http://zh.wikipedia.org/zh/%E6%9C%80%E5%A4%A7%E4%B8%8B%E7%95%8C
对于第一个问题,kkt条件中只要求lambda_{i}>=0,没有说nu_{i}也要大于0啊,而且你在文章中写的是>0,不是大于等于0,不知道我说的对不。
第二个问题,维基说是“下确界或最大下界被指示为 inf(S),并被定义为小于等于在 S 中的所有数的最大实数”,应该是max minL(x,r,v)吧(不会写latex……)
多谢回复
KTT是对所有的约束条件都适用的,所以所有的拉格朗日乘子都要大于等于0.至于是不是严格的大于0,如果严格的大于就是紧约束(达到约束的边界),否则就是松约束(有没有都没有差别)。我觉得这里影响不大吧...
至于inf还是min...我觉得这里也没太大差别... -_-|| 不过对偶问题一定是最小化的(如果原问题是最大化的).
准确的说,这里如果标准化原问题是最小化的,那么对偶问题一定是最大化的....