最近园主尝试在网上买了一件二手物品。首先因为它还有点值钱,所以园主才花心思去卖掉,否则直接送人就好了对吧。
卖二手物品主要集中在各种分类网站上,园主选了几个:58同城、百姓网、赶集网和淘宝二手(闲鱼)。这几个网站买东西的模式都差不多,反正大概写写找张照片挂上去就好了。但是定价呢?
首先参考同类产品的定价不是?大概搜了搜别人的定价,嗯,估摸一下可以类似产品取个均值,于是楼主写了个1500块。
然后我们知道需求曲线: q = q(p),大概长成百度说的这个样子:(不要问我为什么Q在X轴....经济学家永远是奇怪的一群人)。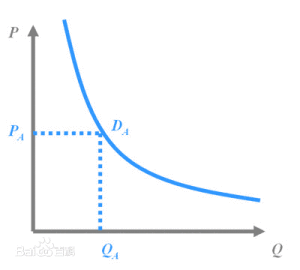 我们假设在每个平台上每天搜这个产品关键字的人有 X个,搜到之后点进去看的占10%,如果价格高于他的预期效用(最高购买价)就不买,如果低于预期效用就不买。那么就可以大概算一下园主的waiting time的问题就是,愿意出价的人>=1个。即落在上述需求曲线那条虚线水平线上面对应的累计Q1>=1,虽然实际上应该是离散的但是就写个积分形式吧:
我们假设在每个平台上每天搜这个产品关键字的人有 X个,搜到之后点进去看的占10%,如果价格高于他的预期效用(最高购买价)就不买,如果低于预期效用就不买。那么就可以大概算一下园主的waiting time的问题就是,愿意出价的人>=1个。即落在上述需求曲线那条虚线水平线上面对应的累计Q1>=1,虽然实际上应该是离散的但是就写个积分形式吧: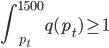
假设上述需求曲线成立,那么对于每天的这个积分大于1的概率(此时可以把所有访客看作服从这么一个需求曲线作为概率分布密度函数的分布,那么每天卖掉的概率就应该是
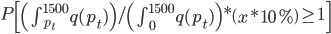
然后x可以是对于t有个随机性的,理论上我们可以算出来到底第T天累计的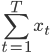 会使得上述累加概率和足够大。假设卖掉的话我就拿到当时的价格
会使得上述累加概率和足够大。假设卖掉的话我就拿到当时的价格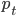 ,卖不掉的话就得到0,这样我就可以算一个对于等待时间的期望
,卖不掉的话就得到0,这样我就可以算一个对于等待时间的期望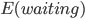 或者期望效用。鉴于我是没有耐心的,也不知道上述各个参数的具体值,所以我打算采用一种策略来估计上述系数的实际值:
或者期望效用。鉴于我是没有耐心的,也不知道上述各个参数的具体值,所以我打算采用一种策略来估计上述系数的实际值:
- 统计每天的页面点击量,然后如果当天没有卖掉,第二天就降价
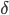 ,降价的幅度可以通过梯度下降计算出来(类似于降价拍卖原理)。
,降价的幅度可以通过梯度下降计算出来(类似于降价拍卖原理)。
于是我就洋洋得意的开始执行此战略。
你问我实际的执行情况?呵呵,我就第一天挂了1500,第二天脑袋一抽写了个1300,然后就卖出去了...然后就没有然后了....反正卖掉了,做人要讲诚信...
5 replies on “论网上集市二手物品的定价模式”
我只是好奇,卖掉的是什么东东,感觉买二手比买新货难多了。。。
哈哈哈哈,不告诉你。
卖的是一手好萌!
人家是很严肃认真的在论述一个学术模型好不好?
市场微观结构的低频版