≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记（十四）

开春，复课。

一句无关的话...今天打开Google Reader看到7月份要关的提示，无限悲伤。看着落园若干RSS源里面累计800+的读者，只能说句bless...2008年开始使用，到现在，伴我度过了多少读书时光呀。不过确实也衰落了，高峰的时候一个RSS源就有600+读者，现在也只剩一半了。写博客，越来越像一件出力不讨好的事情了。

--------正文开始---------

提升与梯度树

1. Boost(AdaBoost)

这里讲的AdaBoost是仅针对二类分类器的提升。大致的思想就是，给我一个弱分类器，还你一个强分类器。听起来蛮神奇的对不对?

先说算法实现。

第一步：初始化。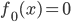,权重初始值 。

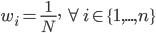第二步：迭代。

for m = 1 to M

• 根据已有算法（即弱分类器）和{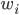}得到一个分类器.
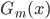• 计算误差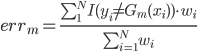：，这里我们把权重进行归一化。
• 计算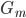权重：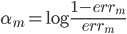
• 修改样本权重：

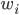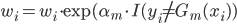
也就是说，我们不断的生成新的权重，当分类器分错的时候更改权重。

第三步：输出。最终的分类器为前面的加权。

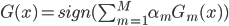
这样就实现了从一个弱分类器改善到一个强分类器。这里弱分类器是指误差比随机猜的1/2少一点。

另注：在修改权重那一步的时候，也可以定义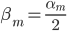，然后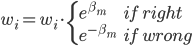，这样在最后的时候也可以改成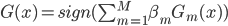。总之这里的直觉是，如果分对了，那么权重下降；反之，分错的时候这些样本的权重上升。最后take average就可以了。

2. 自适应基函数模型、前向分布算法

之所以上面又引入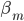，便是为了更好地理解这一类模型：自适应基函数模型。

1. 我们称 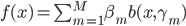为基函数模型，其中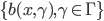成为基函数基。注意这里和GLM有很大的不同，广义线性模型后面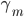的为确定的。

2. 前向分步算法。

数据集记作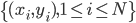。定义一个损失函数，比如常见的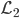均方误差,

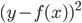，或者0-1准则。

然后步骤为：

• 初始化：
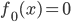
• 迭代：For m=1 to M，
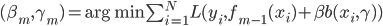
• 令。
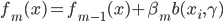• 输出。

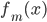这样我们就把这个最优化问题转变成了M步，每步只做一个参数的最优化（近似方法）。

3. 指数损失函数与AdaBoost

有了这么一个一般性的框架，我们就可以套用具体的形式。

1. 定义指数损失函数： 。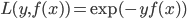

2. 两类分类、指数损失函数的自适应基函数模型。

前向分布算法：

(i)

定义

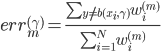
这样上式就可以化作

(ii) 固定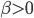，优化.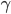

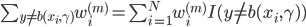
然后最小化，则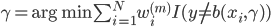。假定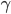已被优化，然后继续。

(iii)优化。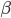

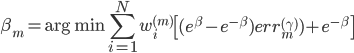
取一阶条件FOC，则有

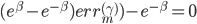
这样最后

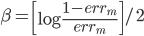
这样就看出来上面那个AdaBoost里面的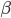是怎么来的了吧?

(iv) 回到AdaBoost

看出来最后的AdaBoost雏形了吧？