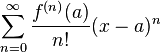众所周知，泰勒展开是数学分析和复变函数幂级数这一章最重要的公式。在复数域内更是任何一个解析函数都有泰勒展开式，这一下子就大大拓宽了函数的范围。
而后在复变有关于泰勒展开的唯一性证明。如果存在数列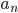
使得
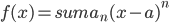则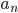必是唯一的。
我们用的教材上证的时候是逐阶求导，个人觉得有些麻烦。其实很简单的一种道理就是因为x的n次幂(n=1,2,...)线性无关，所以若存在数列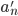
也满足该式，则两式相减可得 
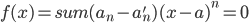。由(x-a)的各次幂线性无关，则可知必有
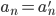。因此唯一性得证。
当时上课给老师说的时候，老师主要提出了两个问题：
1.有限维能不能推广到无线维
可能有限到无限在很多时候是难以直接推广的，但是这里应该没有问题，因为无论如何各项都是一一对应的。
2.函数线性无关怎么证明
其实函数的线性无关指的是在某一定义域内两函数的线性关系不随着其自变量x的取值而改变。因此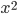
和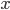
一定会是线性无关的。再由数学归纳法，可证。当然老师当时还提出可以使用范特蒙德行列式证明，确实是数学之间都是相通的啊！
综上，大致写写这些思路，觉得复变函数确实是能开拓一下眼界的，还有泛函里面一些关于基坐标的定义，看来远远不是无源之水啊！
(忽然发现不知怎么将本文归类了……貌似没有数学这一类……读书有感吧！虽说读的是课本。)