例行的废话。刚刚看了一下Google Analytics里面的统计,那篇七天搞定SAS果然不负众望的摘得了(单篇博文)点击量桂冠。意外的是居然有那么多人会点击到“关于我”这个页面...呃,对我这么好奇么?
| 2 | /learning-sas-in-7-days-1/ |
| 3 | /coursera上的r语言课程/ |
| 4 | /r会议小记/ |
| 5 | /使用lyxxetex编译中文tex和输出中文pdf/ |
| 6 | /中文文本聚类小尝试(text-clustering-in-r)/ |
| 7 | /me/ |
| 8 | /?统计学习精要the-elements-of-statistical-learning?课堂笔记(一)/ |
| 9 | /快速将word的doc文件转为latex!/ |
| 10 | /?统计学习精要the-elements-of-statistical-learning?课堂笔记(三)/ |
不过他的后续就比较悲催了,点击量寥寥。然后还不出意外的,weibo超越google成为了流量来源第一:
| 1 | weibo.com / referral |
| 2 | (direct) / (none) |
| 3 | baidu / organic |
| 4 | google / organic |
| 5 | rss / rss |
| 6 | r-ke.info / referral |
| 7 | cloudlychen.net / referral |
| 8 | h2w.iask.cn / referral |
| 9 | so.360.cn / referral |
| 10 | yihui.name / referral |
果然最近墙发威比较厉害...google啊google...
另外,出乎意料的是一些旧文反而受欢迎,哎~还好看到《统计学习精要(The Elements of Statistical Learning)》课堂笔记系列一直有点击,也算是这一系列写的比较值得吧。今天继续。
----------------笔记开始-----------------
貌似是第五章,不过老师一直在讲一些非常基础的数学预备工具:基展开与正则化,其中用到泛函概念若干。我不知道该开心呢,还是不开心呢,还是开心呢,毕竟泛函学过,毕竟泛函忘得也差不多了...
1. 预备知识
在P维欧氏空间内,我们定义两个运算:加法(x+y)和数乘(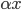 ),然后定义一下函数空间:
),然后定义一下函数空间: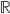 上的平方可积函数
上的平方可积函数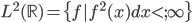 ,同样的定义加法和数乘:f+g和
,同样的定义加法和数乘:f+g和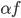 ).
).
接下来还有若干概念...呜呼:
- 线性组合:
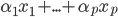
- 线性独立
- 线性子空间:我们可以定义线性子空间,
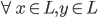 , 有
, 有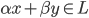 .
. - 基
- 维数
这些概念连上运算加法和数乘一起,构成线性空间。进一步的,我们可以定义内积空间:
- 内积:(离散)
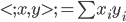 或连续
或连续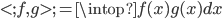
- 之后的正交就很容易定义了:
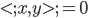 或者
或者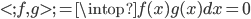
- 还可以定义正交基...
- 还有正交子空间:
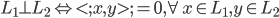
- 正交补:
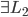 , 使得
, 使得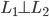 且
且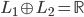 ,比如最简单的二维空间里面,X轴和Y轴...
,比如最简单的二维空间里面,X轴和Y轴... - 范数:
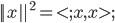
有了范数以后,我们就可以进一步的定义极限:如果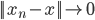 , 则
, 则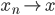 ;或者连续的,
;或者连续的,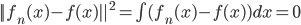 。
。
然后就是闭子空间的概念了:如果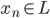 ,且
,且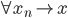 ,则必有
,则必有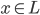 ,即极限点都在空间内。注,在有限维空间内,只有空集和全集既开又闭。
,即极限点都在空间内。注,在有限维空间内,只有空集和全集既开又闭。
还有完备基...总之大致的就是一步步的:定义内积 ->; 内积空间 ->; 存在可数的完备正交基 ->; Hilbert空间(有限维完备空间)
2.B-splines(样条)
2.1 定义
B-splines更多的是一种用离散逼近连续的感觉...好吧我承认我是完全的没有接触过这个东西,扫盲中...
首先,我们有一个闭区间[a,b],然后有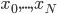 个点聚集在其中,且依次增大。然后我们就可以定义一个函数集合:
个点聚集在其中,且依次增大。然后我们就可以定义一个函数集合: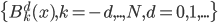 ,然后对于d=0 ,定义分段函数
,然后对于d=0 ,定义分段函数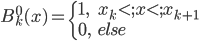 ,然后就可以递归的定义
,然后就可以递归的定义
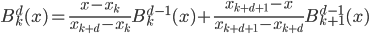
举个例子呢,就有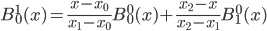 . 这样下去,有:
. 这样下去,有:
- d=0,0阶的时候,只有一段函数上有非零值;
- d=1,1阶的时候,有两段函数有非零值;
- d=2,2阶的时候,有三段函数有非零值...
2.2 性质
- 性质一:
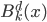 是分段的d次多项式;
是分段的d次多项式; - 性质二:局部性:
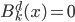 , 当
, 当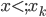 或者
或者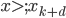 ;
; - 性质三:光滑:
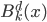 是d-1阶光滑的多项式,即d-1阶导数都等于0;
是d-1阶光滑的多项式,即d-1阶导数都等于0; - 性质四:如果某一函数满足性质三,则必然和
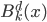 只相差一个常数因子。
只相差一个常数因子。
2.3 d阶B-splines
我们可以用B-splines来逼近任意一个函数,则有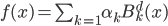 ,从这个角度看B-splines有点基底的味道。从分段多项式,到光滑的分段多项式,再到d-1阶光滑的d次多项式,我们就有了 d阶B-splines...
,从这个角度看B-splines有点基底的味道。从分段多项式,到光滑的分段多项式,再到d-1阶光滑的d次多项式,我们就有了 d阶B-splines...
------笔记结束---------
讲了这么多,我一直在猜这些到底是用来干什么的呢...不知道接下来的哪些内容用到了完备内积空间、基展开和线性逼近呢?
One reply on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(七)”
所有不等号后面都有多余的“;”