鉴于我上周写的[笔记(四)]让很多人反映太枯燥、太无聊(全是公式...可是这就是笔记嘛,又不是写科普文),我努力让这周的笔记除了公式之外多一点直觉和应用层面的点评。
其实[笔记(一)到(二)]中说了很多回归和分类器的不同了,那么在经历了线性回归方法之后,就来说说分类器好了。我原来一直觉得回归和分类器没有什么本质不同的...主要是最常用的分类器logit和probit都是我在学计量的时候学的,那个时候老师只是简单的说,这两个和OLS都是一致的,只是我们想让预测值在0~1之内所以做一下变换。而且我们那个时候也不叫他们分类器,而是叫他们“离散被解释变量模型”。前几个月的时候,看data mining的东西,看得晕晕乎乎的,就跑去问精通此类模型的同事MJ,让他跟我科普了一下午为什么这两个模型大家更经常称之为分类器...汗颜啊,那个时候我才知道原来machine learning是先分supervised learning and unsupervised learning,然后才是 regression v.s. classification, and clustering...疏通了脉络之后,再看《The Elements of Statistical Learning》这本书,就觉得顺畅多了。以前只是零零散散的接触一个个孤立的模型,没有找出一个脉络串起来过,自然也就不知道分别适用于什么场景。
其实我挺想说的是,从econometrics到data mining,远远没有想象的那么简单。数学工具上或许很顺畅,但是思维上的转变还是需要时间和实践的。真是为难坏了我这个学经济学出身的孩子(其实话说回来,我好好的不去研究经济学,好奇什么data mining呀~只能聊以一句“殊途同归”来搪塞自己,对嘛,反正都是doctor of philosophy, 只要是科学,本质的思考方式应该是相通的)。不过搞清楚之后,还是觉得很好玩的——以前是雾里看花,觉得什么都漂亮;现在渐渐的能够分清楚这些美丽之间的差异了,也算是个小进步吧。
再有个小废话...记得上小学的时候,老师问大家“长大了想做什么呀?”,我们总是会特别有出息的回答“科学家~”。那个时候有门课叫做《自然》,老师总给我们讲各种各样的发明,让我们一度觉得这个世界上的问题都被解决完了,还当什么科学家啊。然后老师就给我们讲哥德巴赫猜想,大意是世间还有那么几个悬而未决的皇冠问题,等待大家长大了去攻克。后来,越读书越发现,有那么多问题人们是不知道答案的,只是从 ambiguity -> uncertainty -> possibility -> probability -> certainty (law)一步步的走下去。有那么多问题,其实都是悬而未决的哲学问题,等待着聪明的大脑去回答。这也是越读书越觉得兴奋的缘故吧,越来越多的时候老师会被问倒,然后说“不知道”...然后好奇心就又开始勃勃生长...然后又发现更多的很好玩但没有答案的问题...周而复始,有意思的很。
-------满足大家的八卦之心之后,笔记开始-------
线性分类器
对应原书第四章。
先是来一点直觉上的东西:分类器顾名思义,就是把一堆样本归到不同的类别中去。那么这类模型的几何直觉是什么呢?很简单,空间分割嘛。最直白的,我们有一群人,组成了一个大的群体。然后现在要把大家归为男女两类,那么空间自然就是被分割为两个子空间——男和女了。
线性分类器是什么呢?分割男和女的时候,可能分割是三个一群,五个一簇的,所以非要画分割的界限的话,八成是山路十八弯的...我们以前说过,这类的模型问题就是可能复杂度比较高(比如参数的个数较多),导致就算训练误差小,测试误差不一定小。所以呢,我们希望这个分割界限是直线的(二维平面下)、或者平面的(三维空间中),或者超平面的(高位空间中),这样就比较清晰明了的感觉了。
线性分类器:logit模型(或称logistic regression)
这里也不完全是按照吴老师上课讲的东西了,因为回头再看这本书会发现书中还有一些很好玩的直觉很强的东西。错过不免可惜,一并收纳。
首先换一下记号~我们在前面都用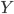 代表被解释变量,从现在开始对于分类问题,我们改用
代表被解释变量,从现在开始对于分类问题,我们改用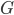 。
。
logit模型下,考虑最简单的分为两类,我们有
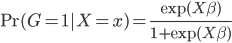
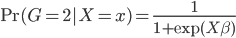
所以有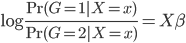
这样,分别属于这两组之间的比例就可以找到一个线性的边界了(注:log为单调变换~不影响结果)。这样变换的目的其实无非是,保证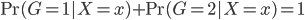 ,而且两个比例之间存在着一种线性的、或者可以通过单调变换成为线性的关系。类似的当然是大名鼎鼎的probit模型,思路是类似的。
,而且两个比例之间存在着一种线性的、或者可以通过单调变换成为线性的关系。类似的当然是大名鼎鼎的probit模型,思路是类似的。
损失函数
显然线性分类器下,在有很多类的情况中,损失函数定义为OLS的残差平方和是没有多大意义的——分类取值只是一个名义量。所以,这里用0-1损失函数:如果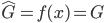 ,那么损失函数=0;否则,就是没预测准,损失函数=1。写为数学形式,就是损失函数
,那么损失函数=0;否则,就是没预测准,损失函数=1。写为数学形式,就是损失函数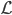 定义为:
定义为:
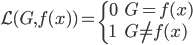
所以我们的目标就是,最小化损失函数的期望:
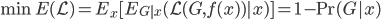
(条件期望迭代)。
LDA:linear discriminant analysis(贝叶斯意义下)
从贝叶斯的角度,我们有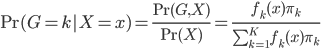 ,
,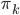
为k出现的概率。
假设X服从联合正态分布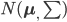 ,那么我们有
,那么我们有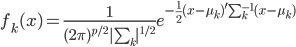 。
。
再假设协方差矩阵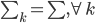 ,所以我们比较两类
,所以我们比较两类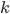 和
和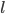 的时候有:
的时候有:

这样就形成了一个x的线性方程,所以我们找到了一个超平面,实现了LDA。
实践中我们需要估计联合正态分布的参数,一般有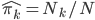 ,其中
,其中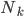 为分类k出现的样本数;
为分类k出现的样本数;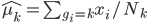 ,即这
,即这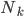 个样本中,x观测值的平均数;
个样本中,x观测值的平均数;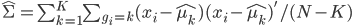 。
。
Fisher视角下的分类器
Fisher提出的观点为,分类器应该尽量使不同类别之间距离较远,而相同类别距其中心较近。比如我们有两群,中心分别为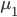
和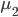 ,那么我们希望
,那么我们希望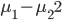 尽量大,同时群内方差
尽量大,同时群内方差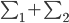
尽量小。通过对x进行投影到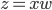 ,我们可以化简的得到
,我们可以化简的得到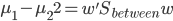
且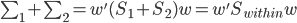 。这样一来,我们的准则就是:
。这样一来,我们的准则就是:
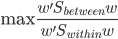
由于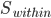 是正定阵,所以我们可以进一步写为
是正定阵,所以我们可以进一步写为
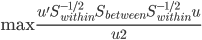
其中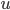 是
是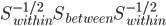 的特征向量。最终可以求的,最优的
的特征向量。最终可以求的,最优的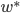 正是
正是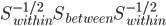 的最大特征向量。
的最大特征向量。
说实话,我对LDA(或者QDA)的理解都非常有限...这本书里面还有一节说到LDA和logit怎么选,我也是大概看了一下没有特别的看明白...笔记只是如实记录,海涵。暂时还不知道讲到Fisher到底是想讲什么...理解力好有限,唉。
------最后的碎碎念------
除了统计学习精要,Coursera的Model Thinking也终于结课了,做完了期末考试卷,感觉心里空空的。这门课真的是开的非常深入浅出,覆盖了这么多学科、问题的各种模型,非常有助于逻辑思考和抽象。只是多少有些遗憾的,很多东西来不及细细回味,听过了视频就忘了,没有努力的去理解那些模型背后的逻辑。这也是导致最终的期末考试做的不怎么好的缘故——我不想去翻课堂视频或者笔记,只是想考验一下自己对于这些模型的理解和记忆能力。事实证明,除了那些跟经济学或者数学紧密相关的模型,其他的都多多少少记得不是那么清晰了。过阵子应该好好整理一下这门课的笔记,算作是一个良好的回顾吧。
不知道为什么,工作之后再去学这些东西,真的感觉力不从心的时刻多了很多。这半年只有这么区区两门课,就让我觉得有时候不得不强迫自己一下赶上进度,强迫的手段之一就是在落园开始写连载(大家容忍,谢谢~)。不过为了保持一个基本的生活质量,还是应该不时看看这些新东西的,要不生活都腐朽了。