支持向量机——最大边距方法
前言:这节课我人在北京,只能回来之后抄一下笔记,然后对着书和wiki理解一下....有什么错误还请大家及时指出。
------------------------------
1. 背景
- 问题:两类分类问题
- 数据:有标识、有监督
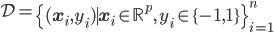
- 模型:
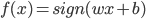 ,线性模型
,线性模型 - 准则:最大边距
先说一下个人理解的SVM的直觉。下图来自wiki。二次元中的SVM就是想找到一条直线(或者对应高维空间下的超平面)来尽可能的分割开两组数据。比如图中H3和H2这两条直线虽然都可以分开这两组数据,但是显然H3离两组数据都远一些——这就是SVM遵循的最大边距准则。
而在实践中,我们把二类分类分别作为正负1,所以两条距离该分割线平行距离1的直线就应景而生。在这两条直线上的点我们称之为支持向量(SV)。
2. 线性可分时的SVM
1) 线性可分:存在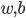 使得
使得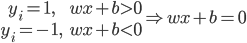 为分割超平面。
为分割超平面。
2) 一个点到超平面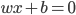 的距离:
的距离:
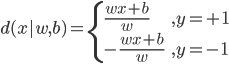
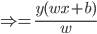
3) 分割超平面的正则表示
数据集到某个超平面的距离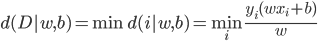 。将
。将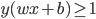 标准化,则
标准化,则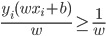 。
。
4) 最大边距准则 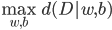
5) 线性可分时的SVM
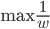
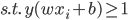
等同于
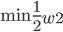
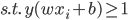
这样就有了一个sign分类器。
6) support vector:分离超平面落在隔离带的边缘,满足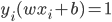 的
的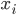 被称为SV。
被称为SV。
7) 优点:
- 对测试误差错识小
- 稀疏性
- 自然直观
- 有效
- 有理论深度(这话的意思是,又可以造出来一堆论文了么?)
3.一般的(线性)SVM
不满足约束的时候,可以做一些放松——引入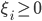 作为松弛变量。
作为松弛变量。
这样原来的最优化问题就变成
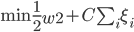
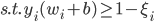
最优的分类器则为
这里大概示意了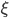 的应用场景。左边是上述完全可分的情况,右边是没法分开,所以我们容忍一些误差,只要误差之和在一个可以接受的范围之内。
的应用场景。左边是上述完全可分的情况,右边是没法分开,所以我们容忍一些误差,只要误差之和在一个可以接受的范围之内。
4.非线性的SVM
这里的直觉大概是,在低维空间较为稠密的点,可以在高维空间下变得稀疏。从而可能可以找到一个高维空间的线性平面,把他们分开。
原来的数据集是: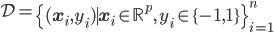
然后定义一个从低维到高维的映射: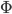 ,使得
,使得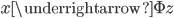 。其中
。其中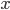 原本属于
原本属于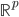 ,此时被映射到一个高维的
,此时被映射到一个高维的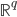 ,可为无限维Hilbert空间(这里我只是照抄笔记...)。
,可为无限维Hilbert空间(这里我只是照抄笔记...)。
映射之后的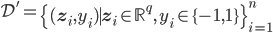 ,之后就是传统的寻找一个线性平面。
,之后就是传统的寻找一个线性平面。
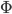 的例子:
的例子:
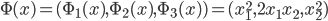 ,这样就打散到一个高维的空间(圆)。
,这样就打散到一个高维的空间(圆)。
下节课是线性SVM的计算。

One reply on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十九):SVM”
园主大人,统计学习也有支持向量机啊。