前两天微博上转出来的,复旦计算机学院的吴立德吴老师在开?统计学习精要(The Elements of Statistical Learning)?这门课,还在张江...大牛的课怎能错过,果断请假去蹭课...为了减轻心理压力,还拉了一帮同事一起去听,eBay浩浩荡荡的十几人杀过去好不壮观!总感觉我们的人有超过复旦本身学生的阵势,五六十人的教室坐的满满当当,壮观啊。
这本书正好前阵子一直在看,所以才会屁颠屁颠的跑过去听。确实是一本深入浅出讲data mining models的好书。作者网站上提供免费的电子版下载,爽!http://www-stat.stanford.edu/~tibs/ElemStatLearn/
从这周开始,如无意外我会每周更新课堂笔记。另一方面,也会加上自己的一些理解和实际工作中的感悟。此外,对于data mining感兴趣的,也可以去coursera听课~貌似这学期开的machine learning评价不错。我只在coursera上从众选了一门 「Model Thinking」,相对来说比较简单,但是相当的优雅!若有时间会再写写这门课的上课感受。笔记我会尽量用全部中文,但只是尽量...
------------课堂笔记开始--------
第一次上课,主要是导论,介绍这个领域的关注兴趣以及后续课程安排。对应本书的第一章。
1. 统计学习是?从数据中学习知识。简单地说,我们有一个想预测的结果(outcome),记为Y,可能是离散的也可能是连续的。同时,还有一些观察到的特征(feature),记为X,X既可能是一维的也可能是多维的。对于每一个观测个体,我们都会得到一个行向量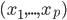 ,对应它的p个特征的观测值,以及一个观测到的结果值
,对应它的p个特征的观测值,以及一个观测到的结果值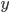 。如果总共有N个个体,那么我们对于每个个体都会得到这些值,则有
。如果总共有N个个体,那么我们对于每个个体都会得到这些值,则有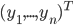 为观测结果的列向量以及X (n*p)矩阵。这样的数据称之为训练数据集(training set)。这里更多是约定一些notation。
为观测结果的列向量以及X (n*p)矩阵。这样的数据称之为训练数据集(training set)。这里更多是约定一些notation。
2. 统计学习分类?一般说来,我们有个观测到的结果Y,然后找到一个适合的模型根据X预测Y,这样的称之为有监督的学习(supervised learning)。而有些时候,Y是无法观测到的,那么只是通过X来学习,称之为无监督的学习(unsupervised learning)。这本书主要侧重有监督的学习。
3. 回归和分类器。这个主要和Y有关。如果Y为离散,比如红黄蓝不同颜色,则称之为分类器(学习模型);反之,若Y为连续,比如身高,则称之为回归(学习模型)。这里更多只是称谓上的区别。
4. 统计学习的任务?预测。通过什么来预测?学习模型(learning models)。按照什么来学习?需要一定的准则,比如最小均方误差MSE,适用于分类器的0-1准则等。基于这些准则、优化过的实现方法称之为算法。
5. 统计学习举例?
分类器:依据邮件发信人、内容、标题等判断是否为垃圾邮件;
回归:前列腺特异抗原(PSA)水平与癌症等因素的关系;
图形识别:手写字母的识别;
聚类:根据DNA序列判断样本的相似性,如亲子鉴定。
6. 课程安排顺序?
第二章,是对于有监督的学习模型的概览。
第三章和第四章将讨论线性回归模型和线性分类器。
第五章将讨论广义线性模型(GLM)。
第六章涉及kernel方法和局部回归。
第七章是模型评价与选择。
第八章是测侧重算法,比如最大似然估计,bootstrap等。本学期预计讲到这里。所以后面的我就暂时不列出了。
目测第二节开始将变得越来越难,前阵子自学第二章痛苦不已啊...一个LASSO就折磨了我好久。当时的读书笔记见:降维模型若干感悟
--------10.15补充---------
上周写的时候只是凭着记忆,笔记没在身边。今天重新翻了翻当时记下的课堂笔记,再补充一些吧。
第九章是可加模型,即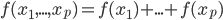
第十章是boosting模型
第十一章讨论神经网络
第十二章讨论支持向量机 (Support Vector Machine)
第十三章设计原型方法(Prototype)
第十四章从有监督的学习转到无监督的学习(即有X有Y->有X无Y)
第十五章讨论随机森林模型(Random Forest)
第十六章是集群学习
第十七章结构图模型
第十八章高维问题(我最近一直念叨的curse of dimensionality...今年搞笑诺贝尔奖也多少与此有关,见 http://www.guokr.com/article/344117/,还有一篇相关的paper)
ps. 吴老师对于随机森林等等模型的评论也挺有意思的,大致是,大家都没搞清随机森林为什么效果这么好...而且这一类模型都是computatoinal intensive的,即有一个非常简单的idea然后借助大量的计算来实现。此外,这类方法更多有“猜”的感觉,无法知道来龙去脉,在现实中显得不那么intuitive...(不像econometrics那般致力于causality呢)。