Stochastic calculus [4th week, Sep]

Today when I was checking my emails, I noticed one ad from The Wharton School of the University of Pennsylvania. There was no doubt that it is the most famous business school throughout the world.  But in fact, at the first glance, I didn't realize that it was Wharton. I just thought that "oh, a school of Upeen“.

Followed its link, I was redirected to its official website, and read the introduction of its applied economics doctoral program. Although I did know that upeen would never give me an admission, I still looked carefully at the details of the program's requirements. Of course, I paid much attention on the mathematical requirements. Some familiar words came into view, like

(1) at least two courses in calculus, (2) linear algebra, (3) differential equations, and (4) probability and statistics. We also recommended that you have taken: (1) real analysis, (2) econometrics, (3) stochastic calculus.

Ok... I have one year left to meet your requirements. However, the fact is, even if I can satisfy all the basic requirements of this program, I am still not competitive enough and I have no money to pay for the tuition. Thus, the final result mentains the same: It has nothing to do with me. Moreover, I would prefer the training of theoretical economics rather than applied economics.

Here I want to say something about "stochastic". Some days ago one junior attracted my interest, not for his intelligence, but for his love of mathematics as a student of economics. I had met hundreds of schoolmates who had a good knowledge of math, either took some classes from the school of mathematics or taught themselves. But most of them were forced to enhance their math ability by the pressure from graduate schools or their advisors. Therefore, the real situation was, they did have some calculation skills after professional math trainings, but seldom did they really have the understanding of the spirit of math.

That boy was different. He didn't got high marks in every class, thereby losing the most valuable testimony of outstanding performance at study. "The only choice for me is to take part in the entrance exams for postgraduate schools ( which is called 'Kao Yan') since my lack of English and GPA ", he laughed at himself when I encouraged him to go abroad. But he told me that he had audited most of the core courses in school of math. That day we talked about a question about matrix, or more specifically, Markov chain. He offered a new solution way, which was really out of my thought. I didn't catch his meaning at first, so he explained it patiently. After that, he recommended me to listen to the course of stochastic process in school of math. To speak honestly, I had some knowledge about stochastic process so I told him. At first he was a little surprised, but soon he gave me an advice for the reason that my understanding of stochastic was not deep enough. Then he gave me a list of the courses and asked whether I would come to the class or not. Unfortunately, the time was conflicted with an other class on Tuesday afternoon. He said that it didn't matter, since I would go to another half  of the course on Thursday and the course was pretty easy. OK, I will certainly do that.

Of course, as an exchange, I provided some suggestion for the economic courses...

Now what I want to say is, why "stochastic" is so important in economics? It seems that every one has an unique answer, so do I. But today the word "stochastic calculus" really makes me confused. After searching on the Internet, I have a basic conception of it. But why it sounds so familiar? ...

Yes, Shige Peng （彭实戈）! And his backward stochastic differential equations! I see... I see...

Appendix:

Some Chinese materials about Stochastic calculus ( Author unknown, sorry! ).

1. 随机微积分（Stochastic Calculus）是干什么的？

一言以蔽之，给随机变量建立一套类似于普通微积分的理论，让我们能够像对普通的变量做微积分那样对随机变量做微积分。

知道了这一点，我们很多时候都可以把普通微积分的思维方式对应到随机微积分上。比如，有些概念，一开始如果我们不理解这个概念起的作用是什么，就可以想想在普通微积分里面跟这个概念相对应的概念的作用。

2. 随即微积分的理论框架是怎么样建立起来的？

一言以蔽之，依样画葫芦。这里的“样”，说的是普通微积分。

在普通微积分里面，最基本的理论基础是“收敛”（convergence）和“极限”（limit）的概念，所有其他的概念都是基于这两个基本概念的。对于随机微积分，在我们建立了现代的概率论体系（基于实分析和测度论）之后，同样的我们就像当初发展普通微积分那样先建立“收敛”和“极限”这两个概念。与普通数学分析不同的是，现在我们打交道的是随机变量，比以前的普通的变量要复杂得多，相应的建立起来的“收敛”和“极限”的概念也要复杂得多。事实上，随机微积分的“收敛”不止一种，相应的“极限”也就不止一种。用的比较多的收敛概念是　convergence with probability 1 (almostsurely) 和　mean-square convergence。

另一个需要新建立的东西是积分变量。在普通微积分里面，积分变量就是一般的实变量，也就是被积函数（integrand）的因变量，基本上不需要我们做什么文章。而随即微积分的积分变量是布朗运动，在数学上严格的定义和构造布朗运动是需要一点功夫的。这个过程是构建随机微积分的的过程中的基本的一环。

“收敛”，“极限”和“积分变量”都定义好了之后，我们就可以依样画葫芦，像普通微积分里面的定义那样去定义接下来的一系列概念。

3. 既然是依样画葫芦，那么跟普通微积分的区别是什么？

最基本的区别在于现在的积分变量是布朗运动，它是时间的一个函数，但是却有一个特殊的性质：布朗运动处处连续但是处处不可导。正是这个特殊的性质使得随即微积分跟普通微积分不同。

在普通微积分里面，我们其实已经接触了用“基本变量的函数”来作为积分变量的情况，比如g(x)是x的函数，我可以用g作为积分变量进行积分：

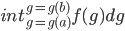
如果g(x)是一个可导的函数,这就是我们在普通微积分中已经解决了的问题，因为dg =g'dx，所以上式可以写成：

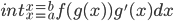
但是对于布朗运动W来说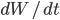，不存在。正因为这个“微分”不存在，导致在普通微积分里面可以直接进行的上述微分运算在随即微积分里面不能直接进行。

比如，在普通微积分里面，有基本的微积分公式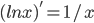

因而.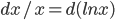

但在随机微积分里面则不能对dW/W 进行这样的计算

，

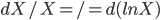因为 ln(X)是不可导的。

这就需要我们建立新的基本运算规则。

４. 随即微积分的基本运算规则是什么？

在普通微积分里面，首先我们定义了牛顿-莱布尼兹公式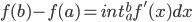

然后我们定义了一系列基本的运算法则，比如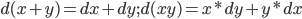

和基本微积分公式，比如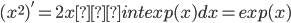。然后我们实际进行微积分运算的时候，主要是把要计算的微分或者积分按照运算法则分解成这些基本的微积分公式，然后把他们用这些基本的微积分公式套进去进行计算。

在随机微积分里面，我们做相同的事情。导致随即微积分和普通微积分在操作上的区别的就是最基本跟牛顿-莱布尼兹公式相对应的新的微积分公式。

普通微积分的牛顿-莱布尼兹公式是由分区间近似求和，然后取极限得到。在随即微积分里面，我们可以用相同的方法来定义积分，但是这个近似的取法不同，会导致计算的结果不同。目前最有实用意义的近似取法是有日本数学家Ito提出的，那就是，在计算某个小区间的对整个积分的贡献的时候，用这个区别的左边界的函数值来代替整个区间的函数值。（Note：在定义普通微积分的时候，我们用的是该区间上任意一点。之所以可以使用该区间上任何一点是因为函数的可导性。而这里，函数不可导，所以不能像普通微积分那样用任意一点的函数值来代替）用这种近似方法，我们可以得到如下基本公式（跟普通微积分里面的牛顿-莱布尼兹公式相对应），Ito公式：

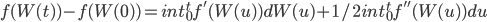
等式右边的第二项是让随机微积分在实际操作上区别于普通微积分的所谓Ito项。

有了Ito公式之后，就可以计算一些基本的常用的微积分公式，比如对于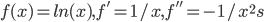，所以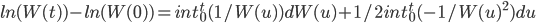

接下来的步骤，就跟普通微积分几乎一模一样，运用运算法则将复杂的微积分分解成基本的微积分，然后套用基本公式。

实际的随机微积分一般都既牵涉到普通变量时间t，又牵涉到随机变量布朗运动W(t)。注意碰到跟t有关的部分就用普通微积分的法则，碰到跟W(t)有关的部分就用随机微积分的法则。

５. 关于随机微分方程

如果你学到随机微分方程了，那么你会遇上随机微积分里面最大的joke，那就是，虽然人们经常把随机“微分”方程挂在嘴上，但实际上人们处理的统统都是随机积分方程。

比如最著名的描述股票运动的方程（其解是Geometric Brownian Motion），我们通常看到下面的形式：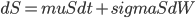
这个貌似微分方程的东西，其实并不是微分方程，原因很简单，S是处处不可导的，所以你不能把dt挪到左边的分母上得到一个类似于dS/dt的东西。所以这跟本就不是一个微分方程，实际上，它是如下积分方程的一个简写而已：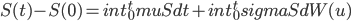
我们通常谈论的随机“微分”方程的general的形式如下：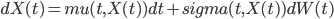

经过刚才的例子，你很容易明白这其实是一个积分方程。

具体解随机“微分”方程的方法没有什么新的东西，做法都跟普通的常微分方程和偏微分方程一样，只不过在所有涉及到以W为变量的微分和积分的时候，都要套用Ito积分的公式。

正如解析方法在常微分方程和偏微分方程里面能解决的问题很有限一样，解析方法在随机“微分”方程里面能做的事情也很有限，实际工作中主要用的数值方法。直接解随机微分方程的数值方法其实就是模拟。模拟主要分强近似和弱近似，前者模拟大量的符合该微分方程的过程，然后根据模拟的这些过程来计算统计值。后者也模拟大量的过程，但这些过程并不严格符合方程所描述的过程的性质，而只是在某些方面（比如终点时刻的值的期望和方差）趋近于方程所描述的过程。

随机微分方程的数值解基本上就是常/偏微分方程的数值解的拓展，比如Euler'smethod，操作起来跟常微分方程的Euler's method几乎一模一样。不同之处在于，用Euler's method解常微分方程，这种逐步往后计算每个点的值的过程只需要进行一次。而在解随机微分方程的时候，每一次只得到一个sample process，对于解一个方程，这个过程需要重复很多次。

６. 随机微分方程跟偏微分方程的关系

再次写出随机“微分”方程的general形式

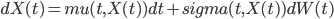
假设我们关心的是X(T)的某个函数的期望值（在实际工作中，我们几乎总是只关心这个，比如E[X(T)]是X(T)本身的期望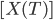，是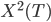的期望），假设这个函数是h，现在要根据t时刻的信息来推断h(X(t))在T时刻的期望。换句话说，我们要计算h(X(T))在时刻t的条件期望，我们把这个条件期望记做g(t,X(t))
.

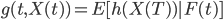很显然这个g也是一个随机过程。进一步的，可以证明，这个在一定的条件下，g是一个martingale。既然是martingale，那么如果计算g的微分，那么微分中的dt项应该为0，这是建立随机微分方程和偏微分方程的最基本出发点。实际上，dg中的dt项为0可以导致如下结论：

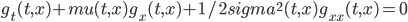
式中的下标表示偏微分。

这样我们就由一个随机微分方程得到了一个偏微分方程。注意这个偏微分方程非常的有用，因为在实际工作中，我们大多数情况下并不关注X(t)作为一个随机过程的种种细节，而更多的只关注他的某些函数的期望和条件期望，比如E[h(X(T))|F(t)]。而上面的这个微分方程，解决的正是这种问题。所以很多时候，面对着一个随机微分方程的问题，我们并不需要真正的去解随机微分方程，而只需要解对应的偏微分方程就可以了。

上面阐述的这层关系叫做Feynman-Kac定理。顺便说一句，在金融中大名鼎鼎的Black-Scholes-Merton微分方程，其实就是Feynman-Kac定理的一个小小应用而已。

如果我们计算不是h(X(T))的条件期望，而是exp(-r(T-t))h(X(T))的条件期望，基于同样的推导，我们可以到类似的偏微分方程：

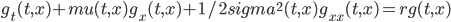
这就是Black-Scholes-Merton微分方程。